Итак, здесь вся информация по вопросам плюс мои ремарки в отдельных случаях. Пока все ответы, несовпадающие с ответами и критериями засчёта считаются условно неправильными.
Ответы команд
Ответы команды "Альтернатива"
капитан Omnicide
1. Нобель
2. Математиков 8, астрологов 12
3. Сосчитайте до трех
4. А-Янус Полуэктович Невстеруев и У-Янус Полуэктович Невстеруев
5. не меньше 5
6. Математику - ПИ, козлику - РОГА
7. Семи слов
8. Клейн вобще не математик
9. А мне все равно, я - e в степени x
10. Беру с собой на самолет бомбу
11. Высшая математика
12. поисковик Гугл (от "гугол")
13. Число Непера
14. Равны нулю
15. k=3
16. X = БРУТТО, Y = ТАРА, Z = НЕТТО
17. Кто имеет, тому дано будет и приумножится, а кто не имеет - у того отнимется и то, что имеет
18. Преувеличение
19. Метод "от противного"
20. Счастливый
21. Потому что интегралы придумали люди
22. Тот, который замечает аналогии между аналогиями
23. Математическое хокку
24. Профессор Мориарти
25. 3$ = 300 центов. А 300 цетов в квадрате = 900$
26. Формулы
27. О мировых войнах
28. Кошка, которая гуляет сама по себе
29. Четки
30. Чтобы привлечь побольше посетителей (теорема Ферма еще не была доказана)
31. Бабочка
32. Трисекция угла
33. Поп и собака
n. С пи.
Ответы команды №3
капитан Дилетант
1. Нобель
2. Наибольшее возможное число математиков 8, астрологов — 10.
3. Сосчитайте до трех
4. А-Янус и У-Янус
5. Пятеро
6. Пи - математику, рога - козлику
7. семи слов.
8. Клейн принадлежит классу не-математиков: Цермело хотел своей задачей сделать нелестный для Клейна вывод, что тот не является математиком.
9. Мне всё равно — я экспонента!
10. всегда вожу с собой бомбу и чувствую себя хорошо
11. Высшая математика
12. Гугл
13. Число Непера
14. равны нулю
15. k=3
16. Х — масса брутто; Y — тара; Z — масса нетто
17. Всякому имеющему дастся и приумножится, а у неимеющего отнимется и то, что имеет.
18. Гипербола
19. Метод доказательства от противного
20. "счастливый"
21. Бог придумал берущиеся интегралы; всё остальное дело рук математиков.
22. Который видит аналогии между аналогиями.
23. Хайку
24. Мориарти
25. 3 доллара = 300 центов. 300^2=90000 центов =900 долларов
26. Формулы
27. О Мировых войнах
28. Кошка, которая гуляет сама по себе
29. Четки
30. Потому что если бы самолет разбился, все бы сочли, что он ее доказал!
31. Бабочка
32. Трисекция угла
33. Поп и собака
n. Спи, моя радость, усни!
Ответы команды №4
капитан FLASH-ka*
1. нобель
2. 12 астрологов и 8 математиков
3.досчитайте до трёх
4. А-Янус У-Янус
5.5
7. из семи слов
8. Клейн не математик
9. e^x
10.вожу с собой одну бомбу
11.высшая математика
14.равны нулю
15.k=3
18.преувеличение
19. доказательство от противного
20.счастливый
21. Бог их берет в численном виде
23.хокку
24.профессор Мориарти
25.перевел доллары в центы
26.формулы
27.мировые войны
28.кошка которая гуляет сама по себе
29.абак
31.бабочка
32.трисекция угла
33. поп, собака
Ответы команды №1
капитан Dieter Zerium
1. Нобель
2. математиков -8
астрономов - 12
3. досчитайте до трех
4. пространство
5. 5
6. Рога
7. максимум из семи слов
8. Клейн - не матиматик
9. а я е^x
10. Всегда вожу с собой бомбу и летаю спокойно
11. Высшая математика
12. Microsoft
14. чисто мнимые
15. 3
16.
17.
18. преувеличение
19. метод от противного
20. трамвайные билеты с симметричными номерами, т.е. одинаково читаются слева направо и справа налево
21 Наши математические затруднения Бога не беспокоят. Он интегрирует эмпирически"
22. аналогиями
23. нелепица
24. Мориарти
25. сын сказал, что заработал 300 центов, а значит отец должен выплатить ему 90000 центов, что равно 900 долларам
26 формул
27.мировую войну
28. Кошка, которая гуляет сама по себе
29. камешки
30. нашёл ошибку
31. бабочка
32. трисекция угла
авторские ответыФестиваль "ЭНИГМА-92" (Тернополь) 1992-01-01
2-й тур
Вопрос 1: Выдающийся шведский математик Миттаг Леффлер очень настойчиво ухаживал за чужой женой. Возможно причина личной неприязни математика и мужа этой женщины была в другом, но, как говорят, именно из-за это конфликта пострадали коллеги Леффлера. Недоразумение загладил американец Джон Чарльз Филд в 1932 году.
Назовите фамилию мужа этой женщины.
Ответ: Нобель. Нобелевская премия математикам не присуждается. Премия Филда – медаль присуждаемая за выдающиеся открытия в области математики с 1932 года.
5 Фестиваль "МАГИ на Воробьевых горах". 1996-09-29
ЧГК среди школьников
Вопрос 2: За круглым столом сидят 12 человек: математики и астрологи. Математики всегда говорят правду, а астрологи не всегда. Каждый сидящий за столом сказал: "Один из моих соседей – математик, а другой – астролог". Назовите наибольшее возможное число математиков и наибольшее возможное число астрологов за этим столом.
Ответ: 8 и 12.
Автор(ы): Максим Поташев
"Бархатный сезон - 2007" (Юрмала) 2007-09-15
1 тур
Вопрос 3: [Раздаточный материал: "x^3 – 6x^2 + 11x – 6 = 0".]
Не волнуйтесь, уважаемые знатоки, вам не обязательно решать это уравнение, хотя его решение и является подсказкой к нашему вопросу. Успокойтесь, расслабьтесь, закройте глаза, [три слова пропущены]. Откройте глаза и заполните пропуск.
Ответ: "Сосчитайте до трех".
Зачёт: "Один, два, три...", "раз, два, три...", "три, два, один..." и т.п.
Автор(ы): Алексей Пасечник (Санкт-Петербург)
Источник(и): Алгебра, учебник для 9 класса.
Комментарии: Корни этого уравнения: 1, 2 и 3. Для тех, кто хорошо учился в школе, не составит труда вспомнить, что сумма и произведение корней этого уравнения равны шести, и, допустив, что автор вопроса не станет издеваться над игроками, предположить, что корни – целые числа.
И вопров №3.
Первая лига Москвы сезона 2001-2002 гг. 2001-01-01
7.2. Вопросы команды В.Назарова
Вопрос 4: Их можно встретить в астрономии и математике. Их составные части в астрономии имеют собственные имена, а в математике отличаются на 2. В астрономии их конечное число, в математике вопрос о конечности их множества до сих пор открыт. Герой одной советской сказки принял за них одного человека. У этого человека было 2 прозвища, отличавшиеся 1 буквой, и эти прозвища Вам и надо будет назвать через минуту.
Ответ: А-Янус и У-Янус.
Автор(ы): Вадим Назаров
Источник(и):
1. СЭС М.; Советская Энциклопедия, 1980г.
2. Школьная Энциклопедия. Математика. М.; Научное издательство "Большая Российская Энциклопедия", 1996 г.
3. А. и Б. Стругацкие "Понедельник начинается в субботу", "Сказка о тройке", Москва, изд. "Книжный сад", 1993.
Комментарии: Речь шла о близнецах. У звезд созвездия Близнецы есть названия: Поллукс и Кастор. В математике близнецы – простые числа, разность которых равна 2. А. Привалов, герой книги "Понедельник начинается в субботу" ("сказки для научных сотрудников младшего возраста") спросил, когда в первый раз увидел Янусов "-близнецы?"
Синхронный кубок Республики Беларусь по ЧГК. Сезон 2004-2005 2004-12-12
1
Вопрос 5: Мебиус на одной своей лекции рассказал притчу о восточном правителе, который оставил свое государство сыновьям, завещав поделить его так, чтобы в случае чего каждый мог придти на помощь другому. Сыновья не смогли выполнить его волю. А сколько их было?
Ответ: Пять.
Автор(ы): Мишель Матвеев (Санкт-Петербург)
Источник(и): М. Гарднер. Математические головоломки и развлечения.
Комментарии: Якобы именно так была впервые сформулирована проблема четырех красок. И вопрос №5.
Ответ «не меньше пяти» считаю неправильным.
Основания:
1. С точки зрения формальной логики он верен, однако в вопросе речь идёт о конкретной ситации: лекции Мёбиуса.
2. Проблема чётырёх красок имеет наглядное обоснование притчей лишь при наличии пяти сыновей. Проблемы пяти красок в топологии не существует и Мёбиусу нелогично добавлять сыновей, так как это убаляет как наглядность притчи ,так и рациональность примера — педагогического подхода, использованног омёбиусом в данном случае.
3. Косвенный указатель - номер вопроса.
Корпоративные турниры "Абсолютно интеллектуальный банк - 2" (АИБ-2) и "Homo Computerus" 2004-03-20
2 тур
Вопрос 6: В пересказе Бориса Заходера "Алисы в Стране Чудес" математик нетривиально разделил кусок пирога между собою и козликом. Что же досталось математику, а что – козлику?
Ответ: Математику – пи, козлику – рога.
Автор(ы): Валерий Якубсон (Самара)
Источник(и): arbuz.narod.ru/y_pipi.htm
"Первый блин" (Великий Новгород) 2006-05-13
3 тур
Вопрос 7: Этот вопрос имеет шанс остаться в истории.
Закончите афоризм математика Хуго Штейнхауса двумя словами: "В истории остаются фразы из...".
Ответ: "... семи слов".
Автор(ы): Роман Оркодашвили (Баку)
Источник(и): "Мастера афоризма", Хуго Штейнхаус.
Комментарии: Все три фразы вопроса, включая афоризм, состоят из семи слов. И вопрос №7
Кубок Полесья-2001, Гомель 2001-05-05
Второй тур
Вопрос 8: Декан математического факультета Геттингена Клейн правил подчиненным, что называется, железной рукой. Приват-доцент Цермело решил насолить строгому администратору и обнародовал такую логическую задачку: "Все математики Геттингена принадлежат к двум классам. Одни делают то, что не нравится им, но нравится Клейну. Другие делают то, что нравится им, но не нравится Клейну. К какому классу относится в таком случае сам Клейн?" Решите и вы эту задачку, учтя, что "ни к какому" – ответ не для математиков...
Ответ: "Клейн – не математик".
Источник(и): "Наука и жизнь". 11/2000, с.43.
Знатоки на Волге. Издалека - долго... 1999 год (N5-N137) 1999-01-01
1
Вопрос 9: Учителя математики, объясняющие начала интегрального и дифференциального исчисления, часто рассказывают такой анекдот. Волею случая два математика оказались в одной палате сумасшедшего дома. Один (видимо, "буйный") в припадке кидается на второго с криком: "Я тебя сейчас проинтегрирую, а потом продифференцирую!" Что ответил ему второй (очевидно, "тихий"), чтобы показать полное свое безразличие?
Ответ: Он ответил: "А я – е в степени икс". Известно, что при интегрировании и дифференцировании экспоненциальной функции (е в степени икс) получается та же экспоненциальная функция – ей все равно.
Автор(ы): Дмитрий Богаевский (Балашиха)
Первый круг чемпионата Харькова по "Брэйн-рингу" сезона 2000/01.
Вторая лига, октябрь-ноябрь 2000 г.
Вопрос 10: Анекдот. "Новый русский" рассказывает: "Я спросил у знакомого математика, какова вероятность того, что в самолет подложат бомбу. Он прикинул, что где-то 0,0001. Тогда я спросил, какова вероятность, что я окажусь в самолете с двумя бомбами на борту. Оказалось, и вовсе ничтожная величина: 0,00000001. С тех пор я...". Закончите фразу.
Ответ: "... всегда вожу с собой бомбу и летаю спокойно".
Автор(ы): Дмитрий Башук
Источник(и): "Телескоп", 14.09.2000 г.
Вопросы Ученого Кота, 1999 г. 1999-01-01
Март 1999.
Вопрос 11: В начале нашего века немецкий профессор Феликс Клейн написал ценную для учителей книгу, название которой переводится как "Элементарная математика с высшей точки зрения". У нас же в стране это название перевели неправильно, что послужило причиной появления термина, которым мы пользуемся до сих пор. Что это за термин?
Ответ: Высшая математика (книгу перевели как "Элементарная математика с точки зрения высшей").
Автор(ы): Константин Алдохин (Великие Луки)
Источник(и): "Знание – сила", 7, 1994, с. 101.
АИСТ-2003 (Американский Интеллектуальный Синхронный Турнир) 2003-01-01
5 тур
Вопрос 12: ЕГО названием стало слегка искаженное слово, придуманное девятилетним племянником одного американского математика. По-видимому, это название подчеркивает его претензии на лидерство. И, надо сказать, он действительно занимает ведущие позиции в мире среди себе подобных. Назовите его.
Ответ: Google.
Автор(ы): Мишель Матвеев (Санкт-Петербург)
Источник(и):
1. xsuseless.narod.ru/u852.htm
2. www.google.com/press/facts.html
Комментарии: Google – искаженное googol (гугол), 10 в степени 100.
Один против дюжины. 2001 год 2001-01-01
Тур 39
Вопрос 13: Услышав одно из названий ЭТОГО, не слишком образованный человек мог бы предположить, что ЭТО имеет нечто общее с числами 13 или 22, хотя на самом деле название происходит от фамилии известного математика. Что же ЭТО?
Ответ: Число е, оно же число Непера.
Автор(ы): Максим Поташев
И вопрос № 13.
Синхронный чемпионат Белоруссии среди школьников. 2002 2002-01-13
2 тур
Вопрос 14: Математический анекдот! Математика спрашивают: "Есть ли крылья у слона?" – "Есть, – отвечает математик, но они..." Закончите фразу двумя словами/
Ответ: "... равны нулю".
Автор(ы): Леонид Климович
Источник(и): Упомянут в вопросе.
Комментарии: Принимать именно в такой формулировке (два слова).
Ответ «чисто мнимые» считаю неправильным.
Основания:
1. "Равны нулю" - более учтойчивое выражение, свойственное языку математики, нежели "чисто мнимые".
2. Мнимые числа существуют в теории (ака корень из -1), однако, того, что равно нулю в математическом понимании нет совсем.
3. Авторский критерий зачёта («Принимать именно в такой формулировке»)
Чемпионат Днепропетровска сезона 2002/03 гг. Высшая лига 2002-01-01
Команда "Flash"
Вопрос 15: Господа знатоки, закончите следующий анекдот. Жили два друга – математик и музыкант. Музыкант не раз предлагал математику сходить на какой-нибудь концерт, но тот всегда отказывался. Однажды музыкант сказал своему другу следующее: "Пойдем, будет выступать прекрасный (слово пропущено) оркестр", после чего математик сразу согласился. После концерта музыкант спросил у математика, понравился ли ему концерт, но тот разочарованно ответил: "Ничего интересного, ведь k равно...". Если вы поняли, какое слово было пропущено, то легко сможете ответить, чему равно k?
Ответ: 3.
Комментарии: Пропущенное слово – "камерный".
Не в том суть ,что три музыканта. Просто, они-то были в трёхмерными...)
"Белые ночи-2002" (Санкт-Петербург) 2002-07-06
4 тур
Вопрос 16: Внимание, линейное уравнение! X-Y=Z. Составить это уравнение было несложно: берем "грубый" X, отбрасываем Y, который как раз и "следует отбросить", и получаем "чистый" Z. Найдите X, Y и Z.
Ответ: брутто, тара, нетто.
Автор(ы): Дмитрий Борок (Самара)
Источник(и): СЭС, ст. "Брутто", "Тара", "Нетто".
Комментарии: В переводе соответственно "грубый" (итал.), "то, что следует отбросить" (араб.), "чистый" (итал.).
Вопрос 17: На доске пишется следующий текст:
dx/dt = a(x-b)
a"0, b"0
Этим дифференциальным уравнением мы попытались выразить идею, которую можно не раз встретить в евангельских притчах – например, в главе 25 Матфея. Мы не будем требовать дословной точности, но все же попытайтесь воспроизвести смысл этой идеи как можно ближе к библейскому тексту.
Ответ: Всякому имеющему дастся и приумножится, а у неимеющего отнимется и то, что имеет.
Зачёт: По смыслу (напр., "У неимущего отнимется, имущему прибавится").
Автор(ы): Дмитрий Жарков
Источник(и):
1. Матфей 25:29 (также Матфей 13:12, Марк 4:25, Лука 8:18, Лука 19:26).
2. Элементарные соображения математического анализа.
Комментарии: Если в начальный момент времени x меньше некоторого критического значения (b), то дальше он будет только падать, а если больше – то только расти.
VII Чемпионат России среди студенческих команд по ЧГК. Москва. 2007-04-21
2 тур
Вопрос 18: [Раздается уравнение "x^2-y^2=1".]
Что Жозеф де Местр назвал ложью благовоспитанных людей?
Ответ: Преувеличение.
Зачёт: Гипербола.
Автор(ы): Мишель Матвеев (Санкт-Петербург)
Источник(и): Душенко К.В. Мысли, афоризмы и шутки знаменитых мужчин. – М.: Эксмо, 2007.
Комментарии: Роздано уравнение гиперболы. Гипербола – преувеличение.
МУБК 2001-2002 2001-01-01
Команда "ДНОГ-2"
Вопрос 19: Английский математик Харди утверждал, что некий мощный метод, часто употребляемый математиками, схож с шахматным гамбитом, но идет дальше, ибо шахматист отдает пешку или фигуру, в то время как математик жертвует всей игрой. Назовите этот метод.
Ответ: доказательство от противного
Вопрос 20: вопрос снят
Спасибо Trotil.
Именно он указал на ошибку в формуле. Перед ней ещё должен быть множитель 1/2Pi ega-math.narod.ru/Quant/Tickets.htm
Перед вами формула, по которой можно вычислить точное количество ТАКИХ ИХ. В среднем же один ОН из восемнадцати является ТАКИМ. Герой одного из романов Переса-Реверте пытался продать коллекцию из 5775 ТАКИХ ИХ. Какой эпитет мы заменили словом "ТАКОЙ"?
Ответ: Счастливый.
Автор(ы): Юрий Дзюбенко (Запорожье)
Источник(и):
1. ru.wikipedia.org/wiki/Счастливый_билет
2. Артуро Перес-Реверте. Клуб Дюма, или Тень Ришелье. – М.: Иностранка, 2003.
Комментарии: Речь идет о счастливых билетах.
Вопросы Дмитрия Жаркова, клуб "Мозговорот", 1998 1998-01-01
Блок 7
Вопрос 21: Как-то раз у Эйнштейна спросили: почему Бог, создав мир логическим и сообразным, допустил, чтобы существовали неберущиеся интегралы – те, решение которых не представляется в виде формулы. Эйнштейн ответил, что Богу эта проблема незнакома. Почему?
Ответ: Если Богу надо взять интеграл, он всегда делает это в численном виде – так можно взять любой интеграл.
Автор(ы): Дмитрий Жарков
Источник(и): math.furman.edu/~mwoodard/ascquote.html (12.06.96)
6-й Чемпионат Одессы по ЧГК 2000-01-01
7-й Тур 12.05.2001 К-да Сигма
Вопрос 22: По определению математика, упомянутому в книге "Юмор, остроумие, творчество" "Математик – тот, кто умеет находить аналогии между утверждениями, математик посильнее видит аналогии доказательств, еще лучший замечает аналогии теорий...". А какой математик, согласно этому же определению, "самый, самый"?
Ответ: "... который между аналогиями видит аналогии"
Автор(ы): Юрий Волошкевич
Источник(и): Лук А.Н. "Юмор, остроумие, творчество" Москва, "Искусство" 1977.
Курск-2006 2006-01-07
5 тур
Вопрос 23:
На фотографии вы видите Дэйва Байера, математика-консультанта фильма "Игры разума", с системой уравнений, которую он придумал для одной из сцен фильма. Байер хотел, чтобы Нэш в фильме предложил студентам для раздумий имеющую реальный глубокий математический смысл, лаконичную и в чем-то парадоксальную задачу. Посмотрите на строки, выражающие ее, и ответьте, математическим ЧЕМ назвали ее в журнале "Science" после выхода фильма.
Ответ: Хокку.
Зачёт: Хайку.
Автор(ы): Евгений Постников (Курск)
Источник(и): Beatiful Mind's Math Guru. // Science, V. 295, 2002. P. 789-791.
Конкурс "Рейтинг-100". 2002 год 2002-01-01
N116 (01/2002)
Вопрос 24: Произошел из хорошей семьи. Получил блестящее образование. Гениальный математик. В 21 год написал трактат о биноме Ньютона, принесший ему мировую известность. В 22 – заведовал кафедрой математики в университете. Через несколько лет ему пришлось уехать в Лондон, где он подрабатывал репетиторством, параллельно создавая дело всей своей жизни. Однако, довершить его не успел – в 1891 году при трагических обстоятельствах был убит в Швейцарии. Как его звали?
Ответ: Профессор Мориарти
Автор(ы): Карен Налбандян (Ереван)
Комментарии: 50 – 6 место
Игросиб-97, Новосибирск. Брейн. 1997-10-04
взрослые команды.
Вопрос 25: Джо попросил у отца 150 долларов, чтобы купить себе новый велосипед. Его отец-математик деньги дать просто так отказался, но предложил такую схему: Джо торгует на улице лимонадом, а в конце рабочего дня отец смотрит, сколько он заработал, и дает ему сумму, равную квадрату этой выручки. В первый день Джо наторговал на три доллара, и папа-математик думал, что легко отделался, пока хитрый сынок не доказал ему, что он неправ. Как Джо смог получить требуемую сумму в первый же день?
Ответ: Он потребовал, чтобы его выручку считали не в долларах, а в центах. Если считать в долларах, 3^2 = 9$, а вот если в центах – 300^2 = 90000, или 900$.
Автор(ы): Дмитрий Жарков
Источник(и): www.iquest.com/new3bin/riddle/lookup?thedate=01... (3.07.96)
2-й этап Кубка Украины 1999-2000. "Январская Ялта - 2000" 2000-01-22
Тур 1.
Вопрос 26: Один издатель сказал известному американскому ученому Стивену Хокингу, что чем больше их, тем меньше читателей. Более того, по его мнению, каждая из них уменьшает читателей вдвое. Назовите их.
Ответ: Формулы.
Автор(ы): Тваскис Алгис (Ереван)
Источник(и): Баландин Р.К. и др. Заглянуть за завесу времени.
2-й чемпионат Южного Кавказа (Супса) 1999-07-23
Запасные вопросы
Вопрос 27: Американский математик Филипп Дэвис уверяет, что первую вели химики, вторую – физики, а третью будут вести математики. О чем он так говорит?
Ответ: О мировых войнах.
Автор(ы): Борис Бурда
Источник(и): math.furman.edu/~mwoodard/ascquotd.html (12.06.96)
Кубок Мордора - 2002 2002-04-06
Дополнительные вопросы
Вопрос 28: Что такое лента Мёбиуса, вы знаете, что такое лист Мёбиуса, вы тоже знаете. Через одну минуту дайте определение кошки Мёбиуса, приведенное на сайте www.luna.ru
Ответ: Кошка, которая гуляет сама по себе
Автор(ы): Михаил Чернышёв
Чемпионат Краснодара по ЧГК. 2002 год 2002-05-12
1
Вопрос 29: Канцелярские счеты – механический арифмометр – электронный калькулятор – компьютер. Восстановите начальное звено, зная, что оно стало прототипом еще одного технического устройства – безостановочного лифта-патерностера, позаимствовавшего у своего предка как принцип действия, так и латинское название.
Ответ: Четки.
Автор(ы): Станислава Бардушко
Источник(и): "Наука и жизнь", 1991, N 12.
Тренировки Бориса Бурды. 1993 1993-01-01
1 тур
Вопрос 30: В 1927 году великий математик Гильберт должен был читать лекцию в Лоренцевском институте. Вылетая туда, он предварительно телеграфировал тему своей лекции: "Доказательство теоремы Ферма", но прочел совершенно другую лекцию. Почему он так поступил?
Ответ: Если бы самолет разбился, все были бы уверены, что он доказал теорему Ферма.
Автор(ы): Борис Бурда
VII Чемпионат России среди студенческих команд по ЧГК. Москва. 2007-04-21
1 тур
Вопрос 31:
Перед вами чертеж, используемый при формулировке классической геометрической теоремы. Назовите животное, название которого упоминается в названии этой теоремы, или аксессуар, название которого в нем также упоминается.
Ответ: Бабочка.
Автор(ы): Мишель Матвеев (Санкт-Петербург)
Источник(и): ru.wikipedia.org/wiki/Теорема_о_бабочке
Комментарии: По внешнему сходству получившегося чертежа с бабочкой теорема так и называется – "теорема о бабочке".
"Город героев - 2006" (Волгоград) 2006-09-30
3 тур
Вопрос 32:
Теорема Морлея утверждает, что если из каждой вершины треугольника провести определенным образом по два луча, то точки пересечения смежных лучей образуют равносторонний треугольник. Эта удивительная теорема была открыта очень поздно, в 1904 году. Причина в том, что геометры с некоторого времени стали избегать задач, в которых фигурирует... Что?
Ответ: Трисекция угла.
Автор(ы): Мишель Матвеев (Санкт-Петербург)
Источник(и): Г. Коксетер, С. Грейцер. Новые встречи с геометрией.
Комментарии: Два луча, проводимые из каждой вершины, разбивают угол на три равные части – именно такого условие теоремы Морлея.
VII Открытый Кубок России по ЧГК 2005-12-04
1 тур
Вопрос 33: ЭТО используется, например, в теореме Вейерштрасса для построения целой функции по заданным корням. Известны и литературные примеры ЭТОГО, как ни странно, обычно довольно короткие. Я не прошу привести конец любого из таких примеров. Назовите героя и героиню самого известного из них.
Ответ: Поп, собака.
Автор(ы): Мишель Матвеев (Санкт-Петербург)
Источник(и):
1. "Математическая энциклопедия" Изд-во "Советская Энциклопедия", гл. ред. И.М. Виноградов. Т. 1, стр. 616.
2. Татьяна Бонч-Осмоловская "Фракталы в литературе". www.ashtray.ru/main/texts/experlit/fractallit2....
Комментарии: ЭТО – бесконечное произведение. У целой функции в общем случае бесконечно много корней, и она строится как произведение сомножителей, каждый из которого зависит от одного корня. "У попа была собака" – бесконечное литературное произведение.
Закнчите бескрылку (стих, содержащий известную фразу в необычной трактовке):
Источник(и): www.luna.ru/?page=anekdot
Интернет-чемпионат по бескрылкам ИЧБ-3 2002-01-01
1 тур, "АН-2"
Вопрос 26:
- Скажи мне, а тангенс с нуля возрастает?
- Конечно, родная. Я сплю, извини.
- А синус на минус свой знак изменяет
С нуля же? – Нет, [...]!
Ответ:
с "пи". Моя радость, усни
Автор(ы): Борис Гуревич
Источник(и): С.Свириденко, "Колыбельная".
Если где-т оя ошибся механически - указывайте.
Мораторий с вопросов снят. Публичное обсуждение можно начинать прямо сейчас.
Ответы команд
Ответы команды "Альтернатива"
капитан Omnicide
1. Нобель
2. Математиков 8, астрологов 12
3. Сосчитайте до трех
4. А-Янус Полуэктович Невстеруев и У-Янус Полуэктович Невстеруев
5. не меньше 5
6. Математику - ПИ, козлику - РОГА
7. Семи слов
8. Клейн вобще не математик
9. А мне все равно, я - e в степени x
10. Беру с собой на самолет бомбу
11. Высшая математика
12. поисковик Гугл (от "гугол")
13. Число Непера
14. Равны нулю
15. k=3
16. X = БРУТТО, Y = ТАРА, Z = НЕТТО
17. Кто имеет, тому дано будет и приумножится, а кто не имеет - у того отнимется и то, что имеет
18. Преувеличение
19. Метод "от противного"
20. Счастливый
21. Потому что интегралы придумали люди
22. Тот, который замечает аналогии между аналогиями
23. Математическое хокку
24. Профессор Мориарти
25. 3$ = 300 центов. А 300 цетов в квадрате = 900$
26. Формулы
27. О мировых войнах
28. Кошка, которая гуляет сама по себе
29. Четки
30. Чтобы привлечь побольше посетителей (теорема Ферма еще не была доказана)
31. Бабочка
32. Трисекция угла
33. Поп и собака
n. С пи.
Ответы команды №3
капитан Дилетант
1. Нобель
2. Наибольшее возможное число математиков 8, астрологов — 10.
3. Сосчитайте до трех
4. А-Янус и У-Янус
5. Пятеро
6. Пи - математику, рога - козлику
7. семи слов.
8. Клейн принадлежит классу не-математиков: Цермело хотел своей задачей сделать нелестный для Клейна вывод, что тот не является математиком.
9. Мне всё равно — я экспонента!
10. всегда вожу с собой бомбу и чувствую себя хорошо
11. Высшая математика
12. Гугл
13. Число Непера
14. равны нулю
15. k=3
16. Х — масса брутто; Y — тара; Z — масса нетто
17. Всякому имеющему дастся и приумножится, а у неимеющего отнимется и то, что имеет.
18. Гипербола
19. Метод доказательства от противного
20. "счастливый"
21. Бог придумал берущиеся интегралы; всё остальное дело рук математиков.
22. Который видит аналогии между аналогиями.
23. Хайку
24. Мориарти
25. 3 доллара = 300 центов. 300^2=90000 центов =900 долларов
26. Формулы
27. О Мировых войнах
28. Кошка, которая гуляет сама по себе
29. Четки
30. Потому что если бы самолет разбился, все бы сочли, что он ее доказал!
31. Бабочка
32. Трисекция угла
33. Поп и собака
n. Спи, моя радость, усни!
Ответы команды №4
капитан FLASH-ka*
1. нобель
2. 12 астрологов и 8 математиков
3.досчитайте до трёх
4. А-Янус У-Янус
5.5
7. из семи слов
8. Клейн не математик
9. e^x
10.вожу с собой одну бомбу
11.высшая математика
14.равны нулю
15.k=3
18.преувеличение
19. доказательство от противного
20.счастливый
21. Бог их берет в численном виде
23.хокку
24.профессор Мориарти
25.перевел доллары в центы
26.формулы
27.мировые войны
28.кошка которая гуляет сама по себе
29.абак
31.бабочка
32.трисекция угла
33. поп, собака
Ответы команды №1
капитан Dieter Zerium
1. Нобель
2. математиков -8
астрономов - 12
3. досчитайте до трех
4. пространство
5. 5
6. Рога
7. максимум из семи слов
8. Клейн - не матиматик
9. а я е^x
10. Всегда вожу с собой бомбу и летаю спокойно
11. Высшая математика
12. Microsoft
14. чисто мнимые
15. 3
16.
17.
18. преувеличение
19. метод от противного
20. трамвайные билеты с симметричными номерами, т.е. одинаково читаются слева направо и справа налево
21 Наши математические затруднения Бога не беспокоят. Он интегрирует эмпирически"
22. аналогиями
23. нелепица
24. Мориарти
25. сын сказал, что заработал 300 центов, а значит отец должен выплатить ему 90000 центов, что равно 900 долларам
26 формул
27.мировую войну
28. Кошка, которая гуляет сама по себе
29. камешки
30. нашёл ошибку
31. бабочка
32. трисекция угла
авторские ответыФестиваль "ЭНИГМА-92" (Тернополь) 1992-01-01
2-й тур
Вопрос 1: Выдающийся шведский математик Миттаг Леффлер очень настойчиво ухаживал за чужой женой. Возможно причина личной неприязни математика и мужа этой женщины была в другом, но, как говорят, именно из-за это конфликта пострадали коллеги Леффлера. Недоразумение загладил американец Джон Чарльз Филд в 1932 году.
Назовите фамилию мужа этой женщины.
Ответ: Нобель. Нобелевская премия математикам не присуждается. Премия Филда – медаль присуждаемая за выдающиеся открытия в области математики с 1932 года.
5 Фестиваль "МАГИ на Воробьевых горах". 1996-09-29
ЧГК среди школьников
Вопрос 2: За круглым столом сидят 12 человек: математики и астрологи. Математики всегда говорят правду, а астрологи не всегда. Каждый сидящий за столом сказал: "Один из моих соседей – математик, а другой – астролог". Назовите наибольшее возможное число математиков и наибольшее возможное число астрологов за этим столом.
Ответ: 8 и 12.
Автор(ы): Максим Поташев
"Бархатный сезон - 2007" (Юрмала) 2007-09-15
1 тур
Вопрос 3: [Раздаточный материал: "x^3 – 6x^2 + 11x – 6 = 0".]
Не волнуйтесь, уважаемые знатоки, вам не обязательно решать это уравнение, хотя его решение и является подсказкой к нашему вопросу. Успокойтесь, расслабьтесь, закройте глаза, [три слова пропущены]. Откройте глаза и заполните пропуск.
Ответ: "Сосчитайте до трех".
Зачёт: "Один, два, три...", "раз, два, три...", "три, два, один..." и т.п.
Автор(ы): Алексей Пасечник (Санкт-Петербург)
Источник(и): Алгебра, учебник для 9 класса.
Комментарии: Корни этого уравнения: 1, 2 и 3. Для тех, кто хорошо учился в школе, не составит труда вспомнить, что сумма и произведение корней этого уравнения равны шести, и, допустив, что автор вопроса не станет издеваться над игроками, предположить, что корни – целые числа.
И вопров №3.
Первая лига Москвы сезона 2001-2002 гг. 2001-01-01
7.2. Вопросы команды В.Назарова
Вопрос 4: Их можно встретить в астрономии и математике. Их составные части в астрономии имеют собственные имена, а в математике отличаются на 2. В астрономии их конечное число, в математике вопрос о конечности их множества до сих пор открыт. Герой одной советской сказки принял за них одного человека. У этого человека было 2 прозвища, отличавшиеся 1 буквой, и эти прозвища Вам и надо будет назвать через минуту.
Ответ: А-Янус и У-Янус.
Автор(ы): Вадим Назаров
Источник(и):
1. СЭС М.; Советская Энциклопедия, 1980г.
2. Школьная Энциклопедия. Математика. М.; Научное издательство "Большая Российская Энциклопедия", 1996 г.
3. А. и Б. Стругацкие "Понедельник начинается в субботу", "Сказка о тройке", Москва, изд. "Книжный сад", 1993.
Комментарии: Речь шла о близнецах. У звезд созвездия Близнецы есть названия: Поллукс и Кастор. В математике близнецы – простые числа, разность которых равна 2. А. Привалов, герой книги "Понедельник начинается в субботу" ("сказки для научных сотрудников младшего возраста") спросил, когда в первый раз увидел Янусов "-близнецы?"
Синхронный кубок Республики Беларусь по ЧГК. Сезон 2004-2005 2004-12-12
1
Вопрос 5: Мебиус на одной своей лекции рассказал притчу о восточном правителе, который оставил свое государство сыновьям, завещав поделить его так, чтобы в случае чего каждый мог придти на помощь другому. Сыновья не смогли выполнить его волю. А сколько их было?
Ответ: Пять.
Автор(ы): Мишель Матвеев (Санкт-Петербург)
Источник(и): М. Гарднер. Математические головоломки и развлечения.
Комментарии: Якобы именно так была впервые сформулирована проблема четырех красок. И вопрос №5.
Ответ «не меньше пяти» считаю неправильным.
Основания:
1. С точки зрения формальной логики он верен, однако в вопросе речь идёт о конкретной ситации: лекции Мёбиуса.
2. Проблема чётырёх красок имеет наглядное обоснование притчей лишь при наличии пяти сыновей. Проблемы пяти красок в топологии не существует и Мёбиусу нелогично добавлять сыновей, так как это убаляет как наглядность притчи ,так и рациональность примера — педагогического подхода, использованног омёбиусом в данном случае.
3. Косвенный указатель - номер вопроса.
Корпоративные турниры "Абсолютно интеллектуальный банк - 2" (АИБ-2) и "Homo Computerus" 2004-03-20
2 тур
Вопрос 6: В пересказе Бориса Заходера "Алисы в Стране Чудес" математик нетривиально разделил кусок пирога между собою и козликом. Что же досталось математику, а что – козлику?
Ответ: Математику – пи, козлику – рога.
Автор(ы): Валерий Якубсон (Самара)
Источник(и): arbuz.narod.ru/y_pipi.htm
"Первый блин" (Великий Новгород) 2006-05-13
3 тур
Вопрос 7: Этот вопрос имеет шанс остаться в истории.
Закончите афоризм математика Хуго Штейнхауса двумя словами: "В истории остаются фразы из...".
Ответ: "... семи слов".
Автор(ы): Роман Оркодашвили (Баку)
Источник(и): "Мастера афоризма", Хуго Штейнхаус.
Комментарии: Все три фразы вопроса, включая афоризм, состоят из семи слов. И вопрос №7
Кубок Полесья-2001, Гомель 2001-05-05
Второй тур
Вопрос 8: Декан математического факультета Геттингена Клейн правил подчиненным, что называется, железной рукой. Приват-доцент Цермело решил насолить строгому администратору и обнародовал такую логическую задачку: "Все математики Геттингена принадлежат к двум классам. Одни делают то, что не нравится им, но нравится Клейну. Другие делают то, что нравится им, но не нравится Клейну. К какому классу относится в таком случае сам Клейн?" Решите и вы эту задачку, учтя, что "ни к какому" – ответ не для математиков...
Ответ: "Клейн – не математик".
Источник(и): "Наука и жизнь". 11/2000, с.43.
Знатоки на Волге. Издалека - долго... 1999 год (N5-N137) 1999-01-01
1
Вопрос 9: Учителя математики, объясняющие начала интегрального и дифференциального исчисления, часто рассказывают такой анекдот. Волею случая два математика оказались в одной палате сумасшедшего дома. Один (видимо, "буйный") в припадке кидается на второго с криком: "Я тебя сейчас проинтегрирую, а потом продифференцирую!" Что ответил ему второй (очевидно, "тихий"), чтобы показать полное свое безразличие?
Ответ: Он ответил: "А я – е в степени икс". Известно, что при интегрировании и дифференцировании экспоненциальной функции (е в степени икс) получается та же экспоненциальная функция – ей все равно.
Автор(ы): Дмитрий Богаевский (Балашиха)
Первый круг чемпионата Харькова по "Брэйн-рингу" сезона 2000/01.
Вторая лига, октябрь-ноябрь 2000 г.
Вопрос 10: Анекдот. "Новый русский" рассказывает: "Я спросил у знакомого математика, какова вероятность того, что в самолет подложат бомбу. Он прикинул, что где-то 0,0001. Тогда я спросил, какова вероятность, что я окажусь в самолете с двумя бомбами на борту. Оказалось, и вовсе ничтожная величина: 0,00000001. С тех пор я...". Закончите фразу.
Ответ: "... всегда вожу с собой бомбу и летаю спокойно".
Автор(ы): Дмитрий Башук
Источник(и): "Телескоп", 14.09.2000 г.
Вопросы Ученого Кота, 1999 г. 1999-01-01
Март 1999.
Вопрос 11: В начале нашего века немецкий профессор Феликс Клейн написал ценную для учителей книгу, название которой переводится как "Элементарная математика с высшей точки зрения". У нас же в стране это название перевели неправильно, что послужило причиной появления термина, которым мы пользуемся до сих пор. Что это за термин?
Ответ: Высшая математика (книгу перевели как "Элементарная математика с точки зрения высшей").
Автор(ы): Константин Алдохин (Великие Луки)
Источник(и): "Знание – сила", 7, 1994, с. 101.
АИСТ-2003 (Американский Интеллектуальный Синхронный Турнир) 2003-01-01
5 тур
Вопрос 12: ЕГО названием стало слегка искаженное слово, придуманное девятилетним племянником одного американского математика. По-видимому, это название подчеркивает его претензии на лидерство. И, надо сказать, он действительно занимает ведущие позиции в мире среди себе подобных. Назовите его.
Ответ: Google.
Автор(ы): Мишель Матвеев (Санкт-Петербург)
Источник(и):
1. xsuseless.narod.ru/u852.htm
2. www.google.com/press/facts.html
Комментарии: Google – искаженное googol (гугол), 10 в степени 100.
Один против дюжины. 2001 год 2001-01-01
Тур 39
Вопрос 13: Услышав одно из названий ЭТОГО, не слишком образованный человек мог бы предположить, что ЭТО имеет нечто общее с числами 13 или 22, хотя на самом деле название происходит от фамилии известного математика. Что же ЭТО?
Ответ: Число е, оно же число Непера.
Автор(ы): Максим Поташев
И вопрос № 13.
Синхронный чемпионат Белоруссии среди школьников. 2002 2002-01-13
2 тур
Вопрос 14: Математический анекдот! Математика спрашивают: "Есть ли крылья у слона?" – "Есть, – отвечает математик, но они..." Закончите фразу двумя словами/
Ответ: "... равны нулю".
Автор(ы): Леонид Климович
Источник(и): Упомянут в вопросе.
Комментарии: Принимать именно в такой формулировке (два слова).
Ответ «чисто мнимые» считаю неправильным.
Основания:
1. "Равны нулю" - более учтойчивое выражение, свойственное языку математики, нежели "чисто мнимые".
2. Мнимые числа существуют в теории (ака корень из -1), однако, того, что равно нулю в математическом понимании нет совсем.
3. Авторский критерий зачёта («Принимать именно в такой формулировке»)
Чемпионат Днепропетровска сезона 2002/03 гг. Высшая лига 2002-01-01
Команда "Flash"
Вопрос 15: Господа знатоки, закончите следующий анекдот. Жили два друга – математик и музыкант. Музыкант не раз предлагал математику сходить на какой-нибудь концерт, но тот всегда отказывался. Однажды музыкант сказал своему другу следующее: "Пойдем, будет выступать прекрасный (слово пропущено) оркестр", после чего математик сразу согласился. После концерта музыкант спросил у математика, понравился ли ему концерт, но тот разочарованно ответил: "Ничего интересного, ведь k равно...". Если вы поняли, какое слово было пропущено, то легко сможете ответить, чему равно k?
Ответ: 3.
Комментарии: Пропущенное слово – "камерный".
Не в том суть ,что три музыканта. Просто, они-то были в трёхмерными...)
"Белые ночи-2002" (Санкт-Петербург) 2002-07-06
4 тур
Вопрос 16: Внимание, линейное уравнение! X-Y=Z. Составить это уравнение было несложно: берем "грубый" X, отбрасываем Y, который как раз и "следует отбросить", и получаем "чистый" Z. Найдите X, Y и Z.
Ответ: брутто, тара, нетто.
Автор(ы): Дмитрий Борок (Самара)
Источник(и): СЭС, ст. "Брутто", "Тара", "Нетто".
Комментарии: В переводе соответственно "грубый" (итал.), "то, что следует отбросить" (араб.), "чистый" (итал.).
Вопрос 17: На доске пишется следующий текст:
dx/dt = a(x-b)
a"0, b"0
Этим дифференциальным уравнением мы попытались выразить идею, которую можно не раз встретить в евангельских притчах – например, в главе 25 Матфея. Мы не будем требовать дословной точности, но все же попытайтесь воспроизвести смысл этой идеи как можно ближе к библейскому тексту.
Ответ: Всякому имеющему дастся и приумножится, а у неимеющего отнимется и то, что имеет.
Зачёт: По смыслу (напр., "У неимущего отнимется, имущему прибавится").
Автор(ы): Дмитрий Жарков
Источник(и):
1. Матфей 25:29 (также Матфей 13:12, Марк 4:25, Лука 8:18, Лука 19:26).
2. Элементарные соображения математического анализа.
Комментарии: Если в начальный момент времени x меньше некоторого критического значения (b), то дальше он будет только падать, а если больше – то только расти.
VII Чемпионат России среди студенческих команд по ЧГК. Москва. 2007-04-21
2 тур
Вопрос 18: [Раздается уравнение "x^2-y^2=1".]
Что Жозеф де Местр назвал ложью благовоспитанных людей?
Ответ: Преувеличение.
Зачёт: Гипербола.
Автор(ы): Мишель Матвеев (Санкт-Петербург)
Источник(и): Душенко К.В. Мысли, афоризмы и шутки знаменитых мужчин. – М.: Эксмо, 2007.
Комментарии: Роздано уравнение гиперболы. Гипербола – преувеличение.
МУБК 2001-2002 2001-01-01
Команда "ДНОГ-2"
Вопрос 19: Английский математик Харди утверждал, что некий мощный метод, часто употребляемый математиками, схож с шахматным гамбитом, но идет дальше, ибо шахматист отдает пешку или фигуру, в то время как математик жертвует всей игрой. Назовите этот метод.
Ответ: доказательство от противного
Вопрос 20: вопрос снят
Спасибо Trotil.
Именно он указал на ошибку в формуле. Перед ней ещё должен быть множитель 1/2Pi ega-math.narod.ru/Quant/Tickets.htm
Перед вами формула, по которой можно вычислить точное количество ТАКИХ ИХ. В среднем же один ОН из восемнадцати является ТАКИМ. Герой одного из романов Переса-Реверте пытался продать коллекцию из 5775 ТАКИХ ИХ. Какой эпитет мы заменили словом "ТАКОЙ"?
Ответ: Счастливый.
Автор(ы): Юрий Дзюбенко (Запорожье)
Источник(и):
1. ru.wikipedia.org/wiki/Счастливый_билет
2. Артуро Перес-Реверте. Клуб Дюма, или Тень Ришелье. – М.: Иностранка, 2003.
Комментарии: Речь идет о счастливых билетах.
Вопросы Дмитрия Жаркова, клуб "Мозговорот", 1998 1998-01-01
Блок 7
Вопрос 21: Как-то раз у Эйнштейна спросили: почему Бог, создав мир логическим и сообразным, допустил, чтобы существовали неберущиеся интегралы – те, решение которых не представляется в виде формулы. Эйнштейн ответил, что Богу эта проблема незнакома. Почему?
Ответ: Если Богу надо взять интеграл, он всегда делает это в численном виде – так можно взять любой интеграл.
Автор(ы): Дмитрий Жарков
Источник(и): math.furman.edu/~mwoodard/ascquote.html (12.06.96)
6-й Чемпионат Одессы по ЧГК 2000-01-01
7-й Тур 12.05.2001 К-да Сигма
Вопрос 22: По определению математика, упомянутому в книге "Юмор, остроумие, творчество" "Математик – тот, кто умеет находить аналогии между утверждениями, математик посильнее видит аналогии доказательств, еще лучший замечает аналогии теорий...". А какой математик, согласно этому же определению, "самый, самый"?
Ответ: "... который между аналогиями видит аналогии"
Автор(ы): Юрий Волошкевич
Источник(и): Лук А.Н. "Юмор, остроумие, творчество" Москва, "Искусство" 1977.
Курск-2006 2006-01-07
5 тур
Вопрос 23:
На фотографии вы видите Дэйва Байера, математика-консультанта фильма "Игры разума", с системой уравнений, которую он придумал для одной из сцен фильма. Байер хотел, чтобы Нэш в фильме предложил студентам для раздумий имеющую реальный глубокий математический смысл, лаконичную и в чем-то парадоксальную задачу. Посмотрите на строки, выражающие ее, и ответьте, математическим ЧЕМ назвали ее в журнале "Science" после выхода фильма.
Ответ: Хокку.
Зачёт: Хайку.
Автор(ы): Евгений Постников (Курск)
Источник(и): Beatiful Mind's Math Guru. // Science, V. 295, 2002. P. 789-791.
Конкурс "Рейтинг-100". 2002 год 2002-01-01
N116 (01/2002)
Вопрос 24: Произошел из хорошей семьи. Получил блестящее образование. Гениальный математик. В 21 год написал трактат о биноме Ньютона, принесший ему мировую известность. В 22 – заведовал кафедрой математики в университете. Через несколько лет ему пришлось уехать в Лондон, где он подрабатывал репетиторством, параллельно создавая дело всей своей жизни. Однако, довершить его не успел – в 1891 году при трагических обстоятельствах был убит в Швейцарии. Как его звали?
Ответ: Профессор Мориарти
Автор(ы): Карен Налбандян (Ереван)
Комментарии: 50 – 6 место
Игросиб-97, Новосибирск. Брейн. 1997-10-04
взрослые команды.
Вопрос 25: Джо попросил у отца 150 долларов, чтобы купить себе новый велосипед. Его отец-математик деньги дать просто так отказался, но предложил такую схему: Джо торгует на улице лимонадом, а в конце рабочего дня отец смотрит, сколько он заработал, и дает ему сумму, равную квадрату этой выручки. В первый день Джо наторговал на три доллара, и папа-математик думал, что легко отделался, пока хитрый сынок не доказал ему, что он неправ. Как Джо смог получить требуемую сумму в первый же день?
Ответ: Он потребовал, чтобы его выручку считали не в долларах, а в центах. Если считать в долларах, 3^2 = 9$, а вот если в центах – 300^2 = 90000, или 900$.
Автор(ы): Дмитрий Жарков
Источник(и): www.iquest.com/new3bin/riddle/lookup?thedate=01... (3.07.96)
2-й этап Кубка Украины 1999-2000. "Январская Ялта - 2000" 2000-01-22
Тур 1.
Вопрос 26: Один издатель сказал известному американскому ученому Стивену Хокингу, что чем больше их, тем меньше читателей. Более того, по его мнению, каждая из них уменьшает читателей вдвое. Назовите их.
Ответ: Формулы.
Автор(ы): Тваскис Алгис (Ереван)
Источник(и): Баландин Р.К. и др. Заглянуть за завесу времени.
2-й чемпионат Южного Кавказа (Супса) 1999-07-23
Запасные вопросы
Вопрос 27: Американский математик Филипп Дэвис уверяет, что первую вели химики, вторую – физики, а третью будут вести математики. О чем он так говорит?
Ответ: О мировых войнах.
Автор(ы): Борис Бурда
Источник(и): math.furman.edu/~mwoodard/ascquotd.html (12.06.96)
Кубок Мордора - 2002 2002-04-06
Дополнительные вопросы
Вопрос 28: Что такое лента Мёбиуса, вы знаете, что такое лист Мёбиуса, вы тоже знаете. Через одну минуту дайте определение кошки Мёбиуса, приведенное на сайте www.luna.ru
Ответ: Кошка, которая гуляет сама по себе
Автор(ы): Михаил Чернышёв
Чемпионат Краснодара по ЧГК. 2002 год 2002-05-12
1
Вопрос 29: Канцелярские счеты – механический арифмометр – электронный калькулятор – компьютер. Восстановите начальное звено, зная, что оно стало прототипом еще одного технического устройства – безостановочного лифта-патерностера, позаимствовавшего у своего предка как принцип действия, так и латинское название.
Ответ: Четки.
Автор(ы): Станислава Бардушко
Источник(и): "Наука и жизнь", 1991, N 12.
Тренировки Бориса Бурды. 1993 1993-01-01
1 тур
Вопрос 30: В 1927 году великий математик Гильберт должен был читать лекцию в Лоренцевском институте. Вылетая туда, он предварительно телеграфировал тему своей лекции: "Доказательство теоремы Ферма", но прочел совершенно другую лекцию. Почему он так поступил?
Ответ: Если бы самолет разбился, все были бы уверены, что он доказал теорему Ферма.
Автор(ы): Борис Бурда
VII Чемпионат России среди студенческих команд по ЧГК. Москва. 2007-04-21
1 тур
Вопрос 31:
Перед вами чертеж, используемый при формулировке классической геометрической теоремы. Назовите животное, название которого упоминается в названии этой теоремы, или аксессуар, название которого в нем также упоминается.
Ответ: Бабочка.
Автор(ы): Мишель Матвеев (Санкт-Петербург)
Источник(и): ru.wikipedia.org/wiki/Теорема_о_бабочке
Комментарии: По внешнему сходству получившегося чертежа с бабочкой теорема так и называется – "теорема о бабочке".
"Город героев - 2006" (Волгоград) 2006-09-30
3 тур
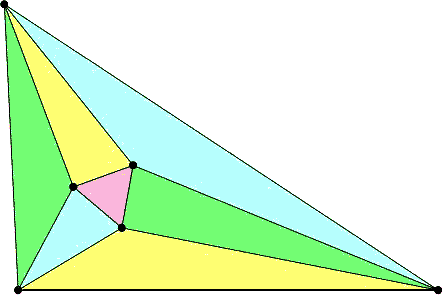
Вопрос 32:
Теорема Морлея утверждает, что если из каждой вершины треугольника провести определенным образом по два луча, то точки пересечения смежных лучей образуют равносторонний треугольник. Эта удивительная теорема была открыта очень поздно, в 1904 году. Причина в том, что геометры с некоторого времени стали избегать задач, в которых фигурирует... Что?
Ответ: Трисекция угла.
Автор(ы): Мишель Матвеев (Санкт-Петербург)
Источник(и): Г. Коксетер, С. Грейцер. Новые встречи с геометрией.
Комментарии: Два луча, проводимые из каждой вершины, разбивают угол на три равные части – именно такого условие теоремы Морлея.
VII Открытый Кубок России по ЧГК 2005-12-04
1 тур
Вопрос 33: ЭТО используется, например, в теореме Вейерштрасса для построения целой функции по заданным корням. Известны и литературные примеры ЭТОГО, как ни странно, обычно довольно короткие. Я не прошу привести конец любого из таких примеров. Назовите героя и героиню самого известного из них.
Ответ: Поп, собака.
Автор(ы): Мишель Матвеев (Санкт-Петербург)
Источник(и):
1. "Математическая энциклопедия" Изд-во "Советская Энциклопедия", гл. ред. И.М. Виноградов. Т. 1, стр. 616.
2. Татьяна Бонч-Осмоловская "Фракталы в литературе". www.ashtray.ru/main/texts/experlit/fractallit2....
Комментарии: ЭТО – бесконечное произведение. У целой функции в общем случае бесконечно много корней, и она строится как произведение сомножителей, каждый из которого зависит от одного корня. "У попа была собака" – бесконечное литературное произведение.
Закнчите бескрылку (стих, содержащий известную фразу в необычной трактовке):
Источник(и): www.luna.ru/?page=anekdot
Интернет-чемпионат по бескрылкам ИЧБ-3 2002-01-01
1 тур, "АН-2"
Вопрос 26:
- Скажи мне, а тангенс с нуля возрастает?
- Конечно, родная. Я сплю, извини.
- А синус на минус свой знак изменяет
С нуля же? – Нет, [...]!
Ответ:
с "пи". Моя радость, усни
Автор(ы): Борис Гуревич
Источник(и): С.Свириденко, "Колыбельная".
Если где-т оя ошибся механически - указывайте.
Мораторий с вопросов снят. Публичное обсуждение можно начинать прямо сейчас.
@темы: Что? Где? Когда?







 Рифма присутствует
Рифма присутствует


