Это, конечно, пока всё предварительно, сами понимаете: скандалы, расследования, формы ответов...

Ну а сейчас выдыхаем и читаем авторские ответы с комментариями.
Я поздравляю вас с окончанием третьего турнира по математическому ЧГК в сообществе «Поп-математика для взрослых детей»

читать дальшеЛетний Днепрофест - 2011. 2 тур. 2011-06-26
Вопрос 3: Внимание, словом "ИКС" мы заменили три слова.
Министр финансов Великобритании Гордон Браун во время визита в школу признался, что он не ИКС и этот факт не помешал ему стать министром финансов. Назовите того, кто ИКС в известном детском стихотворении.
Ответ: Папа у Васи.
Комментарий: ИКС — "силен в математике". На уроке математики признался, что не силен в математике, но это не помешало стать министром финансов.
Источник(и):
1. www.q-news.ru/?art=534
2. deniskastories.narod.ru/slyhano.html
Автор: Александр Чижов (Харцызск)
Чемпионат Торонто - 2007/08. 8 тур. "Веретено". 2008-04-27
Вопрос 11:
Раздаточный материал
Первая формула: 9 + 9*9
Вторая формула: 9 + 9/9
Некоторый предмет, увиденный автором вопроса, похож на множество себе подобных, но вместо обычных надписей на нем несколько формул из трех девяток. Таких, например, как розданные вам. Правда, первой формулы там нет. А вот вторая — есть. Напишите формулу, которая находится чуть выше и правее второй формулы.
Ответ: 99/9.
Комментарий: Это часы, на который числа от 1 до 12 выражены формулами из трех девяток. 9 + 9/9 = 10, 99/9 = 11.
Источник(и):

Автор: Алекс Покрас
X Открытый Чемпионат Москвы по "Брэйн Рингу" среди школьников и студентов. Студенты. Бой 11.. 2001-12-16
Вопрос 2: Голландский физик Гендрик Лоренц нашел соотношение между плотностью вещества и его преломляющей способностью. Несколько ранее эту же формулу, но совершенно другим путем получил датский физик. За формулой утвердилось двойное название. Открытие этой формулы является любопытным случаем с точки зрения теории вероятности. Как называется эта формула?
Ответ: Формула Лоренца-Лоренца (фамилия датского физика тоже была Лоренц).
Автор: Вадим Ефимов
Тюменский марафон - 2010. 6 тур. 2010-05-01
Вопрос 24:
Перед вами формула, предложенная компанией "Parker" в 1970-х годах. Назовите компонент, который предпочитает вносить в эту формулу один из подчиненных М.
Ответ: Водка.
Комментарий: Это юмористическая формула рецепта коктейля Мартини: 3,5 части джина и половина части вермута с четырьмя кубиками льда (вода, H2O, возведенная в куб, = лед), взболтанные тремя движениями (3x360°). Любимый коктейль Бонда — водка-мартини.
Источник(и):
1. ru.wikipedia.org/wiki/Паркер_(бренд)
2. www.bakanov.org/blog/?p=25
Автор: Аркадий Каюгин (Тюмень)
Общемосковский отборочный турнир сезона 2012/13. 3 этап. 2012-10-07
Вопрос 27:
Розданная формула описывает альфу икса. Альфа Икса есть в Рейкьявике. Какие слова мы заменили?
Ответ: Площадь тора.
Зачёт: Площадь Тора.
Комментарий: Формула позволяет найти площадь поверхности тора, которую для краткости нередко называют площадью тора.
Источник(и):
1. ru.wikipedia.org/wiki/Тор_(поверхность)
2. booklists.narod.ru/M_Mathematics/MC_Calculus/MC...
3. www.gulabokin.is/yp_detail.php?tcatid=374&query...
Автор: Станислав Мереминский
Синхронный турнир "Кубок 35", посвященный 35-летию Мишеля Матвеева. 3 тур. Блок Мишеля Матвеева. 2012-03-24
Вопрос 2:
Если спросить вас, какое изменение нужно внести в эту формулу, чтобы получился ОН, вы не ответите, потому что не знаете, что такое ОН. А если попросить вас назвать ЕГО, вы не ответите, потому что не знаете, какое изменение нужно внести. Тем не менее, назовите ЕГО двумя словами.
Ответ: Замкнутый круг.
Комментарий: Если изменить знак < на ≤, то формула будет описывать круг с границей, который в математике называется замкнутым кругом (и является частным случаем замкнутого множества). Круг без границы, напротив, называется открытым. Ситуацию, описанную в вопросе, тоже можно назвать замкнутым кругом.
Источник(и): Общие знания.
Автор: Мишель Матвеев
"Пятый блин" (Великий Новгород). 1 тур. 2010-05-15
Вопрос 5:
Пятый вопрос. Британские ученые вывели формулу получения идеального ИКСА. В формуле, которую вы видите перед собой, например, T [тэ] и m [эм] обозначают температуру, а C [цэ] и k [ка] — консистенцию. Назовите ИКС одним словом.
Ответ: Блин.
Комментарий: Британские ученые вывели формулу получения идеального блина. По их мнению, для того чтобы блин получился идеальным, нужно минимизировать по модулю значение, получаемое при помощи розданной вам формулы. В ней T — температура сковороды, m — идеальная температура сковороды. S — время, в течение которого должно постоять тесто. L — это количество комочков в готовом тесте, а C — это его консистенция, k обозначает идеальную консистенцию. Ну а F — количество переворачиваний блина. Мы рады приветствовать вас на фестивале "Пятый блин"!
Источник(и): blogga.ru/2009/02/25/blin/
Автор: Ирина Емельянова (Рига)
1-й Кубок МГТУ по ЧГК. 1 тур. 1998-05-23
Вопрос 8: Немецкий математик Гаусс в 18 веке предложил формулу для определения этого по григорианскому календарю. Расчет производится по значению математических величин, обозначенных буквами А, Б, В, Г, Д:
А = остатку от деления числа года на 19;
Б = остатку от деления числа года на 4;
В = остатку от деления числа года на 7;
Г = остатку от деления на 30 выражения (19А+15);
Д = остатку от деления на 7 выражения (2Б+4В+6Г+6).
Найденные значения используются для окончательного решения задачи. Если выражение (Г+Д) будет < 9, то это придется на четверть в долевом соотношении и соответствующее число даст выражение (22+Г+Д). Если же (Г+Д)>9, то это придется на треть и число будет (Г+Д-9).С 1918 к результату нужно прибавлять 13. А что предлагается рассчитывать по этой формуле?
Ответ: Дату отмечания праздника Пасхи.
Комментарий: В первом случае она приходится на март и рассчитывается по приведенной формуле, а во втором случае она приходится на апрель и тоже рассчитывается по второй формуле.
Источник(и): Энциклопедия праздников. М., 1994 г.
Автор: Дмитрий Смирнов
Кубок Москвы по ЧГК. Гран-При сезона 2003-2004 годов. 8 тур. Команда "Дельта Фи". 2004-02-15
Вопрос 13:
Это всемирное соперничество ведется по параметру, который вы со школы можете оценить по розданной формуле. В 2001 году на первое место, несмотря на то, что у него α отлична от нуля, вышел азиат, переплюнувший своего северного соседа. В результате знаменитый европеец был отодвинут на третье место. Назовите родной город европейца.
Ответ: Женева.
Комментарий: Речь идет о высочайших фонтанах; формулой дается оценка высоты в зависимости от начальной скорости вылета воды и наклона струи (у самого высокого в мире фонтана в Южной Корее наклон достигает 7 градусов, фонтаны в КНДР и Швейцарии вертикальные). Кстати, на туристических сайтах о северокорейском часто забывают, хотя южнокорейский был построен в том числе и в пику ему.
Источник(и):
1. www.turist.ru/news/newsline/arc.shtml?/news/new... (~200 м)
2. www.euroagency.ru/right.asp?sp=5&id=277 (~150 м)
3. geo.1september.ru/article.php?ID=200104004 (~140 м)
Автор: Александр Ершов
IX Чемпионат Украины по ЧГК. Ровно. 6 тур. 2002-10-19
Вопрос 11: В рассказе Станислава Лема "Формула Лимфатера" изобретатель создает механическое сверхсущество, которое способно мгновенно получать информацию об окружающем мире, не пользуясь никакими органами чувств. Тем не менее его возможностям тоже есть пределы. О каком объекте это существо получило подробную и точную информацию спустя 8 минут после своего рождения?
Ответ: О Солнце.
Комментарий: Область познанного расширялась со скоростью света. Свет от Земли до Солнца идет примерно 8 минут.
Источник(и): С.Лем "Формула Лимфатера"
Автор: Мишель Матвеев (Санкт-Петербург)
Открытый чемпионат вузов России по ЧГК. 2013/14. Финал (Нижний Новгород). 4 тур. 2014-03-29
Вопрос 3:
На этом рисунке мы скрыли подписи под человечками, и в том числе неоднократно скрыли X [ведущему: ИКС]. Восстановите подпись под любым человечком в верхнем ряду.
Ответ: Любой из ответов: sin x, cos x, tg x или tan x, ctg x или cot x.
Зачёт: Синус; косинус; тангенс; котангенс.
Комментарий: Все движения повторяют графики различных функций: синус x, косинус x, x по модулю, квадратный корень из x и т.д. В данном случае ИКС — это ИКС.
Источник(и): 9gag.com/gag/838542
Автор: Дмитрий Озернов (Рига)
Кубок Москвы по ЧГК. Гран-При сезона 2011/12 гг. 7 тур. Команда Дмитрия Карякина. 2012-03-24
Вопрос 1: [Нулевой вопрос]
По мнению автора вопроса, если бы талисман компании "Michelin" был разработан студией Артемия Лебедева, он тоже мог бы выполнять свою функцию, но назывался бы не Бибендум, а ИКС. Назовите двумя словами то, неформальным названием чего является ИКС.
Ответ: Гиперболический синус.
Комментарий: Товары студии Лебедева принято называть псевдолатинскими словами (лабиринтус, пазлус). Составленный из шин человечек — символ компании "Michelin" — вполне мог бы называться шинус. Шинус и чосинус — неофициальные названия гиперболических синуса и косинуса, обозначающихся sh(x) и ch(x).
Этим вопросом автор передает привет Евгению Пашковскому, который однажды сказал, что закончит играть в ЧГК, если ему придется играть вопрос с ответом "гиперболический косинус". Однако поскольку такого ответа у нас пока всё же не прозвучало, мы выражаем надежду на то, что Евгений продолжит свои выступления, в том числе и за нашу команду.
Источник(и):
1. store.artlebedev.ru/
2. en.wikipedia.org/wiki/Bibendum
3. ru.math.wikia.com/wiki/Гиперболические_функции
Автор: Дмитрий Карякин
Синхронный турнир "Голливудская весна - 2011". 1 тур. 2011-04-24
Вопрос 8: Надпись на одном юмористическом рисунке утверждает, что в НЕМ нет места косинусам. Где именно?
Ответ: В Городе Грехов.
Комментарий: По-английски он звучит как Sin City. Sin — математическое обозначение синуса.
Источник(и): www.a-comics.ru/comics/limitman/126
Автор: Олег Фея (Днепродзержинск — Долгопрудный)
Синхронный турнир "Кубок 359". 1 тур. 2015-01-30
Вопрос 9: В математическом анекдоте Фурье умирает, и вскоре из его могилы начинают доноситься странные звуки, что-то вроде: "Синус икс... плюс два косинус икс... плюс три пятых синус двух икс..." и так далее. Вызванный на место происшествия профессор успокаивает публику. Закончите его фразу одним словом: "Ничего страшного, это просто...".
Ответ: Разложение.
Комментарий: Анекдот основан на двух смыслах слова "разложение": разложение функции в ряд Фурье и разложение мёртвого тела.
Источник(и): koteljnik.livejournal.com/702771.html?thread=21...
Автор: Юрий Выменец
XIV Чемпионат Санкт-Петербурга (2012). 10 тур. "Лимпопо". 2012-11-18
Вопрос 14:
Кривая Лоренца показывает неравенство в доходах населения. Каждая точка на ней соответствует утверждению вроде "20 самых бедных процентов населения получают всего 7 процентов дохода". Чем большенеравенство доходов, тем выше индекс ИКСА. На розданном вам графике этому индексу соответствует длинный вертикальный отрезок. Назовите два слова, которые мы заменили на ИКС.
Ответ: Робин Гуд.
Комментарий: Индекс Робина Гуда равен той доле дохода общества, которую необходимо перераспределить для достижения равенства. Весь график похож на лук.
Источник(и): ru.wikipedia.org/wiki/Кривая_Лоренца
Автор: Александр Колышкин
Чемпионат Харьковской области сезона 2013/14. Высшая лига. Третий этап. 3 тур. 2014-02-16
Вопрос 4:
Перед вами система неравенств, с некоторой точностью определяющая ЕГО форму. Рельеф местности в прилегающей к НЕМУ части парка изменен в целях безопасности. Назовите ЕГО двумя словами.
Ответ: Овальный кабинет.
Комментарий: Поверхность Овального кабинета, в соответствии с названием, имеет форму эллиптического цилиндра. Длина большой полуоси основания составляет 5,45 метра, а малой — 4,4 метра. Высота — 5,6 метра. Рельеф парка в прилегающей к нему части искусственно изменен так, чтобы выпущенная пуля не могла достичь кабинета: она может застрять в дереве, специально приподнятой клумбе, бетонной цветочнице.
Источник(и):
1. ru.wikipedia.org/wiki/Овальный_кабинет
2. www.ohranaprofi.ru/sovet/prezident.htm
Автор: Филипп Кузьмин (Санкт-Петербург)
Синхрон Сергея Николенко. 2 тур. 2014-09-19
Вопрос 4:
Когда Льюиса Кэрролла попросили принять участие в философском симпозиуме, Кэрролл ответил: "Что значат эти тайны для меня, чья жизнь полна индексов и иррациональностей?", а также приложил уравнение. Какой символ мы в нем заменили вопросительным знаком?
Ответ: 3.
Комментарий: Кэрролл не любил философию и теологию, и в ответе, конечно, не обошелся без своего фирменного выпендрежа — уравнение рифмуется с текстом. С "surds", соответственно, рифмуются "eleven thirds".
Источник(и): The Complete Illustrated Lewis Carroll. Wordsworth Library Collection, 2008.
Автор: Сергей Николенко
9-й турнир МГИМО-open (Москва). 3 тур. 2014-03-22
Вопрос 14: Рассказывают, что на двери кафедры дифференциальных уравнений Санкт-Петербургского университета висела надпись "Кафедра ИХ", хотя ИХ на этой кафедре совершенно точно не было. Назовите ИХ одним словом.
Ответ: Дуры.
Комментарий: Словосочетание "дифференциальные уравнения" часто сокращают до "диффуры", а иногда даже до "дуры". Преподавательский состав был, говорят, полностью мужским, что довольно типично для математических дисциплин.
Источник(и): Рассказы старших товарищей по матмеху СПбГУ.
Автор: Мишель Матвеев (Санкт-Петербург)
V Чемпионат Центрально-Европейской лиги России. 5 тур. Курск. 2 тур. 2011-02-26
Вопрос 8: Согласно анекдоту, одной девушке-математику всегда приходилось решать уравнения молча из-за строгого указания мамы. В начале какого произведения можно встретить это указание?
Ответ: Мастер и Маргарита.
Комментарий: Никогда не разговаривайте с неизвестными.
Источник(и): Математики тоже шутят. / Авт.-сост. С.Н. Федин. — М.: Книжный дом "Либроком", 2010. — С. 135.
Автор: Евгений Постников (Курск)
Кубок Провинций - 2011. 1 тур. 2011-10-16
Вопрос 6: [Ведущему: открывающие и закрывающие кавычки обозначить словами "начало формулировки" и "конец формулировки".]
Маленькая дочь профессора Элдридж-Смита предложила свою версию формулировки ЕГО: "[Два слова пропущены] сейчас будет расти". Мы не спрашиваем, кто должен говорить эту фразу. Заполните пропуск абсолютно точно.
Ответ: Мой нос. Незачет: Нос Пиноккио и вообще любой ответ, подразумевающий, что говорится не от первого лица; в таком случае парадокса не получается.
Комментарий: ОН — парадокс лжеца. Элдридж-Смит, профессор логики, рассказал дочке про этот парадокс и попросил придумать свой пример. Если Пиноккио говорит правду, то его нос вырасти не должен, но тогда получается, что он солгал, и нос вырасти должен, и так до бесконечности.
Источник(и): Eldridge-Smith P., Eldridge-Smith V. (2010). The Pinocchio paradox. Analysis, 70(2), p. 212v215.
Автор: Дмитрий Жарков (Новосибирск)
Результат: 91/1081
Синхронный турнир "Ивантеллект-2012". 1 тур. 2012-06-29
Вопрос 8: Парадокс ГрЕллинга делит все прилагательные на два множества. Такие, как "многосложное", "русское" и "трудновыговариваемое", принадлежат к числу самодескриптИвных — обладают тем свойством, которое выражают. А такие, как "немецкое", "однокоренное" и "невидимое", — нет. Какое девятнадцатибуквенное слово является ключевым в парадоксе?
Ответ: НесамодескриптИвное.
Комментарий: Можно ли считать слово, говорящее, что оно себя не описывает, описывающим себя? Своеобразная интерпретация парадокса лжеца.
Источник(и): ru.wikipedia.org/wiki/Самореференция
Автор: Константин Сахаров (Ивантеевка)
Результат: 119/199
XIII Чемпионат Украины по брэйн-рингу (Харьков). Первый этап. 2011-04-23
Вопрос 69: Персонаж диалога Дугласа Хофштадтера участвовал в смешанном одиночном турнире и разделил первое место сам с собой. В качестве приза он получил ЭТО, посеребрённое с одной стороны и позолоченное с другой. Назовите ЭТО двумя словами.
Ответ: Лист Мёбиуса.
Зачёт: Лента Мебиуса.
Комментарий: Парадокс на парадоксе.
Источник(и): Д. Хофштадтер. Гёдель, Эшер, Бах: Эта бесконечная гирлянда (www.flibusta.net/b/198312/read).
Автор: Александр Коробейников (Саратов — Санкт-Петербург)
19-й чемпионат Израиля по ЧГК. 2 тур. 2014-03-22
Вопрос 13:
Перед вами сидящий ИКС. Вероятно, вы видели и сидящего ИГРЕКА. А вот ИГРЕК ИКСА вам едва ли встречался. Какие слова мы заменили на ИКС и ИГРЕК?
Ответ: Максвелл, демон.
Комментарий: "Демон сидящий" — картина Врубеля. Демон Максвелла — гипотетическое существо микроскопического размера, придуманное Максвеллом с целью проиллюстрировать кажущийся парадокс второго начала термодинамики. На фотографии у Максвелла в руках устройство для количественного измерения цвета, так называемый диск Максвелла.
Источник(и): commons.wikimedia.org/wiki/File:YoungJamesClerk...
Автор: Мишель Матвеев (Санкт-Петербург)
III Открытый Кубок Серпухова. 4 тур. 2015-06-27
Вопрос 3: Дуплет. Для получения плюса достаточно написать верный ответ только на второй вопрос.
1. Напишите сценический псевдоним человека, который в шестидесятые годы вел на американском телевидении шоу под названием "Давайте заключим сделку".
2. Подскажем, что Джонни КАрсон — это неправильный ответ. Напишите сценический псевдоним человека, который в шестидесятые годы вел на американском телевидении шоу под названием "Давайте заключим сделку".
Ответ: [Монти] Холл.
Комментарий: Известен так называемый парадокс Монти Холла: игроку предлагается выбрать одну из трех дверей, за одной из которых находится приз. После этого ведущий открывает одну из оставшихся дверей (он всегда может выбрать неправильную) и предлагает изменить свой выбор. С вероятностью две третьих приз окажется именно за третьей дверью. Во второй части вопроса мы тоже убрали один из возможных вариантов ответа.
Источник(и): en.wikipedia.org/wiki/Let%27s_Make_a_Deal
Авторы: Михаил Рыжок, Николай Коврижных
VI ежегодный турнир "День физика" (Москва). 1 тур. 2013-05-17
Вопрос 2: [Ведущему: дать командам тридцать секунд на ознакомление с раздаткой.]
Назовите этот фильм.
Ответ: "Начало".
Зачёт: "Inception".
Комментарий: Перед вами был вопрос в вопросе в вопросе. Ответ на вопрос наибольшей глубины вложенности — "левша". Забавно, что после выхода повести словом "левша" стали, напротив, называть умельца. Ответ на второй вопрос — Мауриц Корнелис Эшер. Ответ на последний вопрос — "Начало". "Морис Фишер" звучит созвучно "Маурицу Эшеру". В фильме есть парадоксы и сцены, напоминающие творения Эшера.
Источник(и):
1. www.kinopoisk.ru/film/447301/
2. ru.wikipedia.org/wiki/Эшер,_Мауриц_Корнелис
3. ru.wikipedia.org/wiki/Левша
Автор: Александр Карчевский (Саратов — Москва)
VI Чемпионат Центрально-Европейской лиги России. 5 тур. Курск. 3 тур. 2012-03-17
Вопрос 2: [Ведущему: стихотворение читать построчно.]
Прослушайте "пирожок" — четверостишие без рифмы:
почтенный старый математик
среди [ПРОБЕЛ] бредет ворчит
элементарные задачи
здесь минус сорок например
Заполните пробел.
Ответ: Могил.
Комментарий: Математик вычитает дату смерти из даты жизни.
Источник(и): www.perashki.ru/piro/21687/
Авторы: Александр Беляев и Наталья Беляева (Веллингтон, Новая Зеландия)
Автор: Константин Науменко (Киев)
"Белые ночи - 2013" (Санкт-Петербург). 5 тур. 2013-07-06
Вопрос 14: [Ведущему: четко прочитать "Джоан", чтобы было понятно, что это женское имя.]
В 1941 году свадьба британского математика и криптографа Джоан Кларк расстроилась по не зависящим от нее причинам, поэтому Вильям Кларк так и не смог назвать себя двумя словами. Какими именно?
Ответ: Тесть Тьюринга.
Комментарий: В 1941 году Тьюринг предложил своей коллеге по работе Джоан Кларк выйти за него замуж, но после его признания в своей гомосексуальности их отношения прекратились. После этого Тьюринг так и не женился, и потому никогда не имел тестя. Алан Тьюринг прославился как математик и криптограф.
Источник(и):
1. en.wikipedia.org/wiki/Alan_Turing#Hut_8_and_Nav...
2. www-history.mcs.st-and.ac.uk/Biographies/Clarke...
Автор: Руслан Горусев (Киев)
Кубок Провинций - 2014. Разминка. 2014-10-19
Вопрос 1: Один сингапурский математик назвал своего сына именем, популярным в Англии. Когда родился еще один сын, он назвал младшего китайским именем. Можно сказать, что оба сына вместе представляют собой смешанный экстремум. Как зовут каждого из сыновей?
Ответ: Макс, Мин.
Зачёт: В любом порядке.
Комментарий: Получилось, что сыновья носят имена — сокращенные обозначения понятий "максимум" и "минимум". Максимин и минимакс в математике — смешанные экстремумы.
Источник(и):
1. Конференция по теории графов, Хайфский университет.
2. dic.academic.ru/dic.nsf/enc_mathematics/2975/
Автор: Владислав Тартаковский (Хайфа)
"Синхрон Мерзлякова - Крупника", ранее известный как "Годный Буцентавр". 3 тур. 2013-12-07
Вопрос 5: Многим наверняка знакомо чувство разочарования, появляющееся после того, как сбылась заветная мечта и стремиться больше не к чему. Татьяна ЯмпОльская считает, что мечта должна быть ЕЮ. Впервые ЕЕ упомянул в третьем веке до нашей эры Аполлоний Пергский. Назовите ЕЕ словом греческого происхождения.
Ответ: Асимптота.
Комментарий: Асимптота кривой — это прямая, к которой упомянутая кривая бесконечно приближается, так ее и не достигая. Аполлоний Пергский — древнегреческий математик.
Источник(и):
1. twitter.com/Poll_in/status/373410607426326528/
2. ru.wikipedia.org/wiki/Асимптота
3. ru.wikipedia.org/wiki/Аполлоний_Пергский
Автор: Максим Мерзляков (Воронеж)
XIV Чемпионат Санкт-Петербурга (2012). 5 тур. "Матвей Вуходай". 07.10.2012 - 18.11.2012
Вопрос 13:
Раздаточный материал
Один раз на 4 951 760 157 141 521 099 596 496 896
Эту соотношение приводит математик Роберт Мартин в одной из глав своей книги, комментируя начало известного произведения. Назовите автора этого произведения.
Ответ: Том Стоппард.
Комментарий: В начале стоппардовского "Розенкранц и Гильденстерн мертвы" Розенкранц 92 раза подряд бросает монетку орлом. Такова, согласно Мартину, вероятность такого события.
Источник(и):
1. Robert Martin, There Are Two Errors in the the Title of This Book, 2012. books.google.ru/books?id=3Cx720fWi4kC&pg=PA67
2. lib.ru/PXESY/STOPPARD/r_g.txt
Автор: Эдуард Шагал
Чемпионат мира по ЧГК (Саранск, 2012). Отборочный этап. 1 тур. 2012-09-08
Вопрос 14:
Генри ПЕригаль СДЕЛАЛ ЭТО, воспользовавшись тем, что изображено на данной картине. В Китае считается, что первым СДЕЛАЛ ЭТО Шан ГАо. Что сделал?
Ответ: Доказал теорему Пифагора.
Комментарий: Изображенный на картине плиточный пол выложен так называемым "замощением Пифагора". Это замощение используется в нескольких доказательствах теоремы Пифагора, одно из которых предложил Перигаль. В Китае распространено мнение, что все важные открытия первыми сделали китайцы, в том числе теорему Пифагора первым сформулировал и доказал древний китайский математик Шан Гао.
Источник(и):
1. en.wikipedia.org/wiki/Pythagorean_tiling
2. en.wikipedia.org/wiki/Pythagorean_theorem#Histo...
Автор: Константин Бриф (Ливермор)
Синхронный турнир "Дворец творчества ЮМЫ", посвященный 25-летию команды "ЮМА" (Санкт-Петербург). 1 тур. 2015-02-14
Вопрос 5: В одном стихотворении описывается ученый. Он держит трех котов, по соседству с ним живет восьмилетний мальчик, а еще он тринадцать раз делал ремонт на даче. Назовите фамилию ученого.
Ответ: Фибоначчи.
Комментарий:
Математик седой Фибоначчи
Свою жизнь и не мыслил иначе:
3 кота, в 5 обед,
Восьмилетний сосед
И 13 ремонтов на даче.
В стихотворении обыгрывается ряд чисел Фибоначчи (3 — 5 — 8 — 13), в котором каждое последующее является суммой двух предыдущих.
Источник(и):
1. pelipejchenko.livejournal.com/437036.html
2. ru.wikipedia.org/wiki/Числа_Фибоначчи
Автор: Михаил Локшин (Санкт-Петербург)
"Знатокиада - 2011" (Всемирные игры знатоков) (Эйлат). Брейн-ринг. Бой за третье место. 2011-12-02
Вопрос 8: Исследователь утверждает, что этот 20-летний молодой человек был задирист, как петух, что и привело к его гибели. Накануне смерти он писал, но место на полях кончалось. Согласно грустной шутке, лужайка около пруда Гласьер стала конечным полем в его жизни. Назовите ЕГО.
Ответ: Эварист Галуа.
Комментарий: Пьер Ферма не единственный французский математик, о котором можно задать вопрос. И не единственный, у которого кончалось место на полях. :-) Конечное поле, или же поле Галуа, — это такая математическая штука, смысла которой автор вопроса все равно не знает (зато его знает второй редактор пакета), но она есть. Фамилия Галуа намекает на галльского петуха. Галуа погиб на дуэли.
Источник(и):
1. Программа на канале "Viasat History".
2. Околонаучный околоюмор автора вопроса.
Автор: Эдуард Голуб (Киев)
Гран-при трех пуантов - 2014/15. Пуант II, также известный как "Кубок Мандельброта". 3 тур. 2015-03-06
Вопрос 8: Мы считаем, что без первого предложения ваши шансы взять вопрос были бы значительно меньше.
ЕГО идеи не получали публичной огласки до тех пор, пока через пятьдесят с небольшим лет после ЕГО смерти не были развиты Лапласом. Назовите ЕГО.
Ответ: [Томас] БАйес.
Комментарий: Теорема БАйеса позволяет определить вероятность некоего события при условии, что произошло другое связанное с ним событие. Без первого предложения в вопросе слишком мало информации, поэтому вероятность его взятия невелика, однако при добавлении подсказки вероятность резко повышается. Во всяком случае, нам так кажется.
Источник(и): ru.wikipedia.org/wiki/Теорема_Байеса
Автор: Максим Мерзляков (Воронеж)
Синхронный турнир "День независимости - 2013". 1 тур. 2013-08-24
Вопрос 3: Президент Никсон в одном из выступлений заявил, что скорость роста инфляции пошла на убыль. В книге "Великая теорема Ферма" говорится, что это был первый случай, когда президент использовал третью ЕЕ в своей кампании. Назовите ЕЕ.
Ответ: Производная.
Комментарий: Инфляция — это производная цены, скорость роста инфляции — это уже вторая производная, а ее прирост или уменьшение — третья.
Источник(и): ega-math.narod.ru/Singh/ch2.htm
Автор: Команда "Drakony Jmovirnosti" (Львов)
"Девятый блин" - "Одиннадцатая Великолукская осень" (Великий Новгород). Финал. 2014-05-17
Вопрос 2:
Вы видите, так сказать, "доказательство" утверждения из строки произведения 1969 года. Воспроизведите это утверждение.
Ответ: "Жираф большой — ему видней!".
Комментарий: В соответствии с теоремой Пифагора расстояние до горизонта для идеально круглой планеты можно вычислить по формуле:
, где R — радиус Земли, а h — высота глаза над поверхностью. Для человека видимость составляет 4,6 км, а для жирафа — почти вдвое больше.
Источник(и):
1. www.outdoors.ru/orient/orient107.php
2. www.kulichki.com/vv/pesni/v-zheltoj-zharkoj-afr...
Автор: Евгений Поникаров (Санкт-Петербург)
"Пущинские просторы - 2013" (Пущино, Московская область). 4 тур. 2013-06-22
Вопрос 11: В вышедшем уже в XXI веке романе шахматистка находит собственное чудесное решение, но вскоре получает тяжелое ранение в голову. Какие три буквы мы заменили в начале одного из слов предыдущего предложения?
Ответ: ф, е, р.
Комментарий: Героиня книги Стига Ларссона — ферматистка: так называют людей, занимающаяся поиском собственного доказательства Великой теоремы Ферма элементарными методами. Как известно, такие попытки не прекратились и после опубликования доказательства Уайлса. Пьер Ферма тоже писал, что у него есть воистину чудесное доказательство... А героиня Ларссона безвозвратно утрачивает свое решение после контузии.
Источник(и): С. Ларссон. Девушка, которая играла с огнем. — М.: Эксмо, 2010.
Автор: Эраст Куненков (Узловая)
Чемпионат Белоруссии по ЧГК среди школьников (Минск). 2 тур. 2012-04-21
Вопрос 12:
На этой картинке из учебника математики мы скрыли четыре символа (во всех трех случаях одни и те же). Напишите их.
Ответ: 3,14.
Зачёт: 3.14.
Комментарий:
Цыпленок пищит: "Пи... Пи... Пи... Пи... Пи...".
Источник(и): А. Мерзляк, В. Полонский, М. Якир. Математика: учебник для шестого класса. — Харьков: Гимназия, 2006. — С. 142.

Автор: Татьяна Лещенко (Харьков)
Благотворительный асинхронный турнир "Играй для жизни". 1 тур. 2014-02-01
Вопрос 2:
Раздаточный материал
Одиночество едва не убило меня. Отри слезы мои. Нет четы ревностнее нас, и пусть опять завидуют нам.
Перед вами начало опубликованного в 1906 году шуточного "Письма математика к жене своей". В этом тексте мы сделали пять обратных замен. Запишите то, что мы заменили.
Ответ: 1, 2, 3, 4, 5.
Комментарий: В исходном тексте письма было "1очество е2 не убило меня. О3 слезы мои" и т.д.
Источник(и):
1. Полный любовный письмовник для молодых людей всех возрастов, желающих одержать победу над женским сердцем. — СПб., 1906.
2. vadim-i-z.livejournal.com/3421563.html
Автор: Александр Шапиро (Ришон ле-Цион)
Синхронный турнир "Нехрустальная сова". 2 тур. 2013-05-10
Вопрос 15: Когда математика Эрдёша спросили, нравится ли ему католический колледж, в котором он учился, он ответил, что там много ИХ. Назовите ИХ.
Ответ: Плюсы.
Источник(и): books.google.ru/books?id=6PVN2-ihczYC&pg=PA21
Автор: Фадаи Мамедов (Баку)
18-й Чемпионат Хайфского клуба. 11 тур. "Варан" и "Технион". 24.11.2012 - 22.12.2012
Вопрос 5: Согласно шутке, ОН, придя в зоопарк, научил слона ковыряться хоботом в носу. В одной из серий "Футурамы" на полке стоит ЕГО пиво. Назовите ЕГО фамилию.
Ответ: Клейн.
Комментарий: Шутка обыгрывает внешний вид "бутылки Клейна". В сериале "Футурама" в серии "The Route of All Evil" на полке показано пиво "Klein's", которое разлито в бутылки Клейна. Бутылка Клейна — это определенная неориентируемая поверхность (то есть двумерное многообразие). Бутылка Клейна впервые была описана в 1882 году немецким математиком Ф. Клейном.
Источник(и):
1. twitter.com/fibrenok/statuses/17536850977213644...
2. ru.wikipedia.org/wiki/Бутылка_Клейна
Авторы: Иван Семушин, в редакции Лидии Иоффе
12-й чемпионат России по ЧГК (Москва). 1 тур. 2012-05-19
Вопрос 11:
Раздаточный материал
* Какое наибольшее количество непересекающихся окружностей единичного радиуса можно разместить на сфере радиуса R?
* Привлечение внимания
* Облегчение процесса выбора
* Увеличение сроков хранения
* Стимуляция потребления
Перед вами примеры ИХ в математике и в маркетинге. Назовите ИХ двумя словами.
Ответ: Задачи упаковки.
Источник(и):
1. ru.wikipedia.org/wiki/Открытые_математические_п...
2. i-marketer.ru/_marketing/strukturnyj-dizajn-upa...
Автор: Дмитрий Мишкин (Киев)
Перед вами примеры ИХ в математике и в маркетинге. Назовите ИХ двумя словами.
Раздаточный материал:
.506
.506127
Считается, что благодаря этим двум числам был открыт ИКС. Автор книги «Несовершенная случайность» Леонард Млодинов замечает, что даже сама история открытия ИКСА показывает ИКС в действии. Какие два слова мы заменили словом ИКС?
Ответ: Эффект бабочки
Комментарий: Млодинов пише, что не примени Лоренц эти незначительные расчёты, он не открыл бы эффект бабочки, давший начало целом унаправлению в математике
Источник: en.wikipedia.org/wiki/Butterfly_effect
Автор: Иван Усачук (Донецк)
1.
Раздаточный материал:
Один из комментаторов данного фото сравнил изображённую девушку с НЕЙ. Вероятно, многие из вас со школы помнят, что ОНА является животным с определёнными свойствами. Ответьте тремя словами, что же это животное делает.
Ответ: Делит угол пополам
Зачёт: Бегает по углам
Источник: ru.wikipedia.org/wiki/Биссектриса
Комментарий: Биссектриса - это такая крыса, которая бегает по углам и делит угол пополам.
Автор: Иван Усачук (Донецк)
Вопрос: говоря о финансовом кризисе некоторые экономисты замечают, что эксперты расчета рисков были зачарованы красотой и повсеместностью ЕГО звона. ОН изображен на немецкой монете 1977 года. Назовите ЕГО двумя словами.
Ответ: Колокол Гаусса
Комментарий: причины кризиса 2007 года лежат за пределами нормального распределения. Монета была выпущена в ГДР к 200-летию со дня рождения Карла Гаусса.

@темы: Вопросы, Люди, Парадоксы, Головоломки и занимательные задачи, Что? Где? Когда?



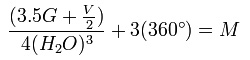
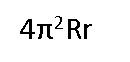













 ? Очень давно думаю над этой задачей, уже мозг об нее сломала.
? Очень давно думаю над этой задачей, уже мозг об нее сломала.



