еще задачка

[=penelopa=]

Одноклеточная амеба каждые 3 часа делится на 2 клетки (пополам). Определить, сколько амеб будет через сутки.

З.ы. по-прежнему ищу похожие задачи, у кого есть, поделитесь, плз))

@темы: задача, алгоритм

---

попалась задача

[=penelopa=]

Богатый дядюшка подарил своему племяннику в день появления на свет 1 доллар. Каждый следующий день рождения он удваивает имеющуюся у племянника сумму и прибавляет к ней столько долларов, сколько племяннику лет.
Определить сумму капитала племянника, подаренную на n-ый день рождения и всего за n лет.

Предлагаю реализовать решение алгоритмом.

У кого есть похожие, интересные задачи, пожалуйста, поделитесь))

@темы: Головоломки и занимательные задачи, алгоритм

---

Счетные палочки Джона Непера

[Amicus Plato]

Не знаю, всем ли известно имя одного из выдающихся математиков, барона Джона Непера (1550-1617) — шотландца по происхождению.
Вот он собственной персоной (с) Википедия:


Знаменит о в первую и в самую основную очередь тем, что изобрел логарифмы!
Можно себе представить, как мучились люди в те времена, производя умножение и деление многозначных чисел. Непер же придумал специальные таблицы, в которых было произведено взаимно однозначное соответствие геометрической прогрессии и арифметической. Причем, естественно, геометрическая прогрессия была исходной. Таким образом, умножению Непер сопоставил гораздо более легкое сложение, а делению, соответственно, — вычитание.
За что всё прогрессивное человечество благодарно ему по сей день.

Но я сейчас буду рассказывать не об этом.
В 1617 году Непер предложил другой, не логарифмический, способ умножения чисел, для которого придумал специальное устройство, получившее название «палочки Непера».
Рассказываю я о нем в связи с записями о фигурных числах. Это еще один способ визуализации арифметики. (Хотя, на самом деле, больше ничего общего с фигурными числами тут нет).

Я узнала о палочках Непера, когда готовила презентацию по истории развития вычислительной техники. Для презентации мне хватило одного слайда с краткой информацией. Сейчас попыталась найти нечто более обширное и ужаснулась: Непер везде упоминается, как правило, как раз в разделе "история вычислительной техники", и пара абсолютно одинаковых абзацев кочует из статьи в статью.
Вот что удалось из всего этого почерпнуть.

Этот «вычислительный инструмент» состоял из брусков с нанесенными на них цифрами от 0 до 9 и кратными им числами. Для умножения какого-либо числа бруски располагали рядом так, чтобы цифры на торцах составляли это число. Ответ можно было увидеть на боковых сторонах брусков.

Вот смотрите: (это самая лучшая из найденных мной картинок):

То есть, как я это рассказывала студентам, это своеобразная трехмерная таблица умножения.
Теперь понимаю, что с трехмерной я погорячилась. Кажется, речь идет о плоском представлении (я думала на этих брусках цифры со всех четырех боковых сторон, но похоже, они только на одной "фронтальной" стороне и на торце).

Полоски с нанесенными на них числами, были еще разделены диагоналями так, что слева (выше) диагонали располагаются десятки, а справа — единицы.
Для получения произведений осуществляется суммирование «вдоль диагоналей».


КАК это происходит, я, если честно, до конца не понимаю. Но судя по тому, что я прочла, четырехзначные числа перемножались с помощью этих палочек шутя.

Помимо умножения, палочки Непера позволяли выполнять деление и извлекать квадратный корень.

Под кат спрячу цитату с одного сайта, постичь которую я не в состоянии)))
Тем не менее, там всё объясняется))
Упражнение для пытливых умов:
Дж. Непер предложил специальные счетные палочки (названные впоследствии палочками Непера), позволявшие производить операции умножения и деления непосредственно над исходными числами. Сверху решетки каждой клетке приписываются цифры А-числа, а справа - цифры В-числа. В каждой (k,j)-клетке решетки записывается результат произведения Rkj=xk*yj соответствующих цифр чисел. При этом число десятков помещается выше диагонали клетки и единиц - ниже диагонали. После заполнения всех клеток решетки производится суммирование S p по наклонным полоскам решетки справа налево с переносом старших разрядов.

Описанный принцип умножения иллюстрируется на примере перемножения чисел 1942 и 54:1942x54=104868. Палочки Непера (в количестве 9; представляют собой своеобразную таблицу умножения, в которой числа записываются в описанной выше клеточной форме) основным назначением имели умножение больших чисел и для операций деления и извлечения корня применялись весьма редко. Сам Непер впоследствии предложил палочки особой конструкции, предназначенные специально для извлечения квадратного корня; они использовались в сочетании с обычными палочками Непера. Наряду с палочками Непер предложил счетную доску для выполнения операций умножения, деления, возведения в квадрат и извлечения квадратного корня в двоичной с.с., предвосхитив тем самым преимущества такой системы счисления для автоматизации вычислений.
Отсюда:
www.tiei.ru/PPage/Pages/7/Consp1/L1-01/COMPUT01...

@темы: Amicus Plato, Люди

---

Из дружественного сообщества))

[Amicus Plato]

Пишет  Серебряный:

31.05.2008 в 01:07

ЛОГИЧЕСКИЕ ОПЕРАТОРЫ
! нет
&! и нет!
!,!&! нет, нет и нет!
. точка.
!&. нет и точка!
= равно
* все
~* не все
*= все равно
~*=? не все ли равно?
*>&> все больше и больше
# точно
!# приблизительно
!#* почти все
$? Деньги есть?
>! Больше нет.
#!? Точно нет?
!4u Не для тебя
&? И чо?
&!? И ничо!

URL записи

@темы: ))), Публикации

---

Фигурные числа III

[Amicus Plato]

Пятиугольные числа
Пятиугольные числа — числа, которые составляют пятиугольники.
По-моему, это образование уже менее естественное, чем все предыдущие, но если вспомнить, какое внимание пифагорейцы уделяли пятиконечной звезде, вписанной в правильный пятиугольник, то удивляться тут нечему.
Вот как они выглядят:
(Знаю, что они даже кривее, чем треугольники... Но что поделать...)


Первые из них легко поддаются счету:
1, 5, 12, 22.
Дальше дело обстоит уже хуже. Следом идут:
35, 51, 70, 92, 117, 145, ...
Если приглядеться, легко проследить закономерность получения пятиугольных чисел:
1
5=1+4
12=1+4+7
22=1+4+7+10
...
В общем виде формула выглядит следующим образом:
P_n = 1+4+7+... (3n-2)
или:
P_n = n*(3n-1)/2

В принципе, можно не ограничивать себя пятью углами и записать формулу k-угольного числа.
К-угольные числа имеют следующий вид (первые два члена у всех последовательностей таких чисел предсказуемы: это единица и само k, а дальше уже нужно пользоваться формулой):
1, k, ... n+(k-2)*n(n-1)/2,...

(Честно говоря, не выводила сама из этой формулы для k=5 формулу пятиугольных чисел. Надеюсь, источники не врут))

Все фигурные числа, которые мы рассматривали до этого, укладываются в плоскости.
Теперь буквально пару слов о числах в трехмерном пространстве.
Они называются телесными числами.
Если мы начнем плоские числа укладывать слоями друг на друга, как раз и получится телесное число.
Самые простые такие числа — кубы, которые образуются из квадратов, уложенных в штабеля.
1, 8, 27, 64,... n³, ...

Уложенные так же прямоугольные числа дадут нам всевозможные произведения своих трех измерений. Не знаю, искал ли кто-нибудь здесь дополнительные закономерности...

Интерес представляют пирамидальные числа.
Они образуются из уложенных друг на друга, а точнее друг под друга треугольных чисел. "Под" — потому что начинают строиться они с вершины.
n-е пирамидальное число состоит из суммы всех треугольных чисел, не превышающих n-е треугольное:
1
1+3=4
1+3+6=10
...
в общем виде:

1+3+6+n*(n+1)/2 = (n-2)*n*(n+1)/6

В заключение расскажу вот какую вещь. (А лучше не буду рассказывать, а процитирую Википедию):

Фигурные числа, по мнению пифагорейцев, играют важную роль в структуре мироздания, поэтому их изучением занимались лучшие математики античности: Эратосфен, Гипсикл, Никомах, Теон Смирнский, Диофант и другие. Последний написал большое исследование о свойствах многоугольных чисел, фрагменты которого дошли до наших дней.

Большой интерес к этим числам издавна проявляла индийская математическая школа.

В Новое время многоугольными числами занимались Ферма, Эйлер, Лагранж, Гаусс и другие. Ферма сформулировал т. н. «золотую теорему»:
Всякое натуральное число — либо треугольное, либо сумма двух или трёх треугольных чисел.
Всякое натуральное число — либо квадратное, либо сумма двух, трёх или четырёх квадратных чисел.
Всякое натуральное число — либо пятиугольное, либо сумма от двух до пяти пятиугольных чисел.
и т. д.

Этой теоремой занимались многие выдающиеся математики, полное доказательство сумел дать Коши.

Красота, не правда ли?!!

@темы: Натуральные числа, Amicus Plato, Люди, античность

---

Фигурные числа II

[Amicus Plato]

Квадратные и прямоугольные числа

Как нетрудно догадаться, квадратные числа — это такие количества камушков, из которых можно выложить квадраты.
То есть, числа, которые можно представить в виде: n*n.


Первые десять квадратов мы все отлично помним со школьных времен. Достаточно представить себе главную диагональ таблицы всё того же Пифагора.
На самом деле почти каждый из нас легко воспроизведет в среднем до двадцати первых квадратов. Дальше уже всё зависит от индивидуальных особенностей памяти, и от того, насколько эти знания для нас актуальны.

Прямоугольные числа — числа, которые представляются в виде: n*(n+1).



Казалось бы, что можно к этому добавить? Всё и так ясно...
Однако добавить можно очень много.

Выпишем квадратные числа:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, ...

Прямоугольные числа:
__ 2, 6, 12, 20, 30, 42, 56, 72, _90, 110, 132, 156, 182, 210, ...

Имея дело с теми и с другими, мы сталкиваемся сразу с двумя парами противоположностей.
Первая, — очевидная пара противоположностей, — квадрат-прямоугольник. Стороны квадрата равны, тогда как стороны прямоугольника различны.
Вторая пара — совсем не так очевидна, но она, наверное, является более важной, и более, что ли, основополагающей.
Это противоположность: четное-нечетное.
Действительно, очень легко убедиться в справедливости следующих двух утверждений.

1. Для любого натурального числа n, сумма первых n нечетных чисел равняется квадратному числу n²:
1 + 3 + 5 + ... + (2n - 1) = n². __________________________________(1)

2. Для любого натурального числа n, сумма первых n четных чисел равняется прямоугольному числу n*(n + 1):
2 + 4 + 6 + ... + 2n = n*(n + 1). __________________________________(2)

Эти утверждения легко доказываются по индукции, однако пифагорейцы прекрасно обходились и без нее.
Давайте посмотрим, как получаются квадратные и прямоугольные числа. То есть, как, зная текущее квадратное (прямоугольное) число, найти следующее.
На рисунках показан процесс, для всех очевидный, но тем не менее очень интересный.

Квадратные числа получаются вот так:


Прямоугольные числа получаются аналогично:


Красными кружочками отмечены новые части, которые прибавляются к уже имеющемуся квадрату (прямоугольнику).

Я неспроста пишу об этом так подробно.
Дело в том, что вот эти красные "уголки" имели для пифагорейцев самостоятельную ценность и назывались гномонами.
Для построения квадратов используются квадратные гномоны.
Для построения прямоугольных чисел — прямоугольные гномоны.

Рассмотрим квадратные гномоны более подробно.
Иногда они рисуются уголками вверх, но я оставлю их уголками вниз. И этому у меня есть особое обоснование. Не знаю, правда, насколько оно соответствует действительности. Если посмотреть определение гномона в любом словаре или энциклопедии, там будет сказано, что это астрономический прибор, состоящий из вертикального штыря, по которому определяют положение солнца. Нечто сродни солнечным часам. (Еще мне кажется, что тот самый приборчик скафис, которым пользовался Эратосфен, (об этом я писала здесь) — ближайший родственник гномона. Но подтвердить это подозрение мне никак не удается.... А опровергнуть я и не пытаюсь...
Так вот, рисую эти, математические, гномоны уголками вниз, потому что мне кажется, что названы они "гномонами" по ассоциации с этими вертикальными штырями, и должны выглядеть именно так!



Из рисунка легко видеть, что идущие друг за другом квадратные гномоны образуют всю последовательность нечетных чисел, больших единицы. (Первая единичка — не гномон, но мне лень ее стирать).
3, 5, 7, 9, ....

Поэтому пифагорейцам даже не нужно было доказывать равенство (1). Это было очевидно из самого построения. Каждый новый квадрат получался из старого прибавлением очередного нечетного числа.

Операция получения большего квадратного числа из меньшего у пифагорейцев выглядела как приложение к меньшему квадрату соответствующего гномона.
Таким образом, любое квадратное число можно породить из единицы посредством последовательного приложения к ней соответствующих квадратных гномонов.
Это и есть "визуальное доказательство" того, что каждое квадратное число является суммой некоторого начального отрезка ряда нечетных чисел.

То же самое относится и к прямоугольным гномонам.



Из этого рисунка видно, что последовательные прямоугольные гномоны соответствуют последовательности четных чисел, больших двойки. (Двойка — не гномон, она хоть и нарисована, но не считается)
Точно так же, как и с квадратами, здесь получение большего прямоугольного числа из меньшего производится с помощью приложения к меньшему числу соответствующего гномона.
Таким образом, любое прямоугольное число можно породить из двойки посредством последовательного приложения к ней соответствующих прямоугольных гномонов.
Тем самым, легко видеть, что каждое прямоугольное число является суммой некоторого начального отрезка ряда четных чисел.
Теперь понятно, почему пифагорейцы утверждали, что "квадрат состоит из нечета, а прямоугольник — из чета".

Продолжение следует.

@темы: Натуральные числа, Amicus Plato, Люди, античность

---

Фигурные числа I

[Amicus Plato]

Пифагор.
Про Пифагора я уже писала: вот здесь.
Речь шла о несоизмеримости гипотенузы и катетов прямоугольного равнобедренного треугольника.
Но это была только самая малость из того, что я хочу рассказать об этом поистине великом человеке.


А сейчас рассказ пойдет о фигурных числах.

Пифагорейцы наделяли числа магическими свойствами. И действительно, в их руках, под их взором, математика обращалась в магию.
Сейчас мы увидим, что самые, казалось бы, "элементарные" — обычные и знакомые нам с детства — натуральные числа — можно увидеть совсем в ином свете.
Сам Пифагор говорил об этом: "Все вещи суть числа". И для пифагорейской школы это был мотто, девиз, которым они руководствовались всегда и везде.

Главной особенностью античной математики был полу-арифметический - полу-геометрический подход к числам.
Пифагорейцы различали треугольные, квадратные, прямоугольные, пятиугольные числа (это, так сказать, двумерные числа, — числа на плоскости). Как производные от них получались кубические и пирамидальные числа.
Не уверена, что перечислила все, но давайте разберемся сначала с этими.

Треугольные числа
Треугольные числа — это такие числа, из которых (имея столько камушков) можно выложить правильные треугольники.
Вот первые четыре числа:

Их значения равны:
Т₁=1, Т₂=3, Т₃=6 и Т₄=10.

Нетрудно продолжить ряд и получить значения следующих треугольных чисел:

Еще парочка...

Т₅=15, Т₆=21, Т₇=27, Т₈=36...

Теперь давайте посмотрим, как они получаются.
Ясно, что геометрически следующее треугольное число получается из предыдущего добавлением "строки", содержащей на один камушек больше, чем самая нижняя "строка" этого предыдущего числа. (Каждая новая строка выделена красным). (Знаю, что картинки малость косоваты, но зато можно не ставить копирайт))) Рисовала сама)))
Таким образом, имеем:

Т_n = 1 + 2 + 3 + 4 +...+ n

С давних времен известно (еще даже до того как девятилетний Карл Фридрих Гаусс открыл сумму первых n членов арифметической прогрессии))), что сумма первых n чисел может быть посчитана следующим образом:

1 + 2 + 3 + 4 +...+ n = ¹/₂ • n(n+1)

Таким образом, треугольное число с номером n вычисляется по этой формуле:
Т_n = ¹/₂ • n(n+1)

Треугольные числа кроме всего прочего являются биномиальными коэффициентами при второй степени икса (в разложении (1 + x)ⁿ по степеням x).

"Число зверя" 666 также является треугольным.

Сумма двух последовательных треугольных чисел даст нам число квадратное.
Формула такова:
T_n + T_{n − 1} = n².
Но об этом — продолжение следует.

@темы: Натуральные числа, Amicus Plato, Люди, античность

---

Виды магических квадратов.

[Trotil]

Магический квадрат — это квадратная таблица n x n, заполненная n² числами, таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях оказывается одинаковой.

Самый известный магический квадрат:

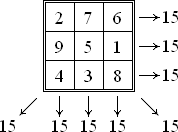
Оказывается, существует целая классификация магических квадратов. Итак:

Нормальный МК - магический квадрат, заполненный целыми числами от 1 до n².

Полумагический квадрат - квадрат, заполненный числами от 1 до n²., называется полумагическим, если сумма чисел по горизонталям и вертикалям равна магической постоянной, а по диагоналям это условие не выполняется.

Aссоциативный, или симметричный МК, такой магический квадрат, у которого сумма любых двух чисел, симметрично расположенных относительно центра квадрата, равна одному и тому же числу: 1+n².

Пандиагональный (дьявольский) МК - такой магический квадрат, в котором сумма чисел по разломанным диагоналям также равна константе квадрата.

Разломанные диагонали:


Идеальный МК - магический квадрат, который одновременно пандиагональный и ассоциативный.

Совершенный МК - магический пандиагональный квадрат порядка 4k, обладающий дополнительными свойствами.

Бимагический квадрат - такой магический квадрат, который остаётся магическим при замене всех его элементов на их квадраты. Бимагических квадратов 3,4,5 порядка не существует.

Мультимагический квадарат - обобщение бимагических квадратов на произвольную степень n.


По этой ссылке можно узнать количестве разных видов МК. Но там не учитываются изоморфные преобразования МК (когда один МК переходит в другой поворотом, сдвигом и т.д.) При подсчете они считались различными.

---

Пятиминутка радости

[cytoex]

Отсюда.

@темы: )))

---

Очередная просьба о помощи ))

[Amicus Plato]

Помните вот эту мою "разработку"?
"Ассоциативная модель памяти".
www.diary.ru/~Organon/p40071949.htm
Я ее несколько формализовала, но пока только на описательном уровне.
Теперь мне нужно построить математический аппарат.
Сейчас попытаюсь вкратце изложить суть. Начну с того, что уже описано в той записи, на которую ссылка.
Вот представьте, что у нас есть множества. Предположим, множества эти существуют в виде мешков. На каждом мешке написано имя множества, соответствующее какому-либо свойству объектов предметной области. Например, мешок с названием "зеленый" или мешок с названием "круглый", и т.д. Мешков таких очень-очень много. Что же в них лежит? В них лежат, предположим, чечевичные зерна. Каждое с надписью. Надпись содержит имя объекта, обладающего данным свойством.
Например (пример тоже старый) хотим мы поместить зеленый ромб в модель, описывающую плоские цветные многоугольники. Модель состоит из множества мешков, на которых написано: "Все стороны равны", "Четыре угла", "Углы попарно равны", "Зеленый", "Выпуклый", "Углы прямые".
Мы возьмем и сосчитаем, сколько мешков (свойств) подходит зеленому ромбу. Из перечисленных шести подходят первые пять. Значит, возьмем пять чечевичных зернышек, обзовем их "Зеленый ромб" или как-то так, чтобы мы знали, что это такое (например, это не абстрактный ромб, а, предположим, что-то конкретное, чему у нас есть имя (в голову ничего не приходит)...), ну, вот, возьмем мы эти подписанные зернышки и разложим по нашим мешкам. И так сделаем с каждым объектом предметной области.
И пусть мешки эти очень удобные: сразу видно, что там внутри лежит.
И вот теперь такой вопрос: можно ли создать метрику на таком пространстве? Можно ли задать расстояние между понятиями?
Должно удовлетворяться очень много требований.
Основные таковы:
1. Чем больше общих мешков у двух объектов А и В, тем расстояние меньше.
2. Чем больше разных мешков у А и В, тем расстояние больше.
3. Чем меньше объектов в каждом конкретном общем для А и В мешке, тем расстояние меньше. Поясню. Если у нас объекты связаны ассоциацией, содержащей 1000 понятий, например, ассоциация, заданная цветом ("зеленый"), то эта ассоциация слаба, и расстояние достаточно велико. А если в мешке всего два зернышка, то вытащив одно, мы моментально узнаем второе: такая ассоциация самая сильная. Расстояние должно быть равно нулю.
4. Аналогичное свойство для мешков с разными свойствами. Чем незначительнее различные свойства (предположим, дело всё в том же цвете), тем меньше эта ассоциация должна влиять на близость. Если же свойства, "разнящие" понятия, т.е. мешки, в которые входит А, но не входит В и наоборот, содержат малое количество объектов, то эти свойства значительны, и расстояние должно сильно увеличиться.
У меня есть две формулы-кандидата для вычисления расстояния, но ни для одной из них не выполняется неравенство треугольника. А без него нет речи о метрике! А метрика тут должна быть! Уж очень красиво выходит!
Вдруг у кого какие-нибудь мысли появятся? А?

@темы: Amicus Plato, Вопросы

---

[Amicus Plato]

Выкладываю ссылку на интереснейшую статью доктора физико-математических наук Владимира Успенского «Апология математики, или О математике как части духовной культуры».
magazines.russ.ru/novyi_mi/2007/11/us10.html
Если вы читаете сообщество давно, вы найдете поразительное количество практически стопроцентного совпадения текста с записями сообщества! Имею в виду не только и не столько содержание, но к нему еще и форму вплоть до метафор и сравнений!
Всё-таки Платоновское царство идей и Ноосфера, видимо, подспудно сильно влияют на наше мышление.

А вот несколько цитат:

***
Неотъемлемой частью цивилизации является то или иное представление об указанном устройстве — хотя бы признаваемое в наши дни совершенно фантастическим, как, например, такое: “А Земля — это только лишь плесень в перевёрнутой неба корзине; звёзды — это свет другого мира, к нам просвечивающий сквозь дно корзины, сквозь бесчисленные маленькие дыры, не затёртые небесной глиной”.

***
Как говорил один из самых крупных математиков XX века Джон фон Нёйман (1903 — 1957): “В конечном счёте, современная математика находит применение. А ведь заранее не ясно, что так должно быть”.

***
“По-видимому, натуральный ряд чисел не представляет из себя абсолютно объективного образования. По-видимому, он представляет собой функцию головы того математика, который в данном случае говорит о натуральном ряде”.

Одним словом, читайте: не пожалеете!

@темы: Поп-математика, Интересные ссылки, Amicus Plato

---

Странное задание

[Atlantida-Smile]

Требуется вычислить: 1/(1*2)+1/(2*3)+1/(3*4)....1/(10*11), а у меня ни одной мысли в голове по этой теме нет, ведь не подходит под определение алгебраической и геометрической прогрессии, да и при помощи факториала не решить....
Если есть идеи и решения объясните пожалуйста мне....

@темы: Головоломки и занимательные задачи, Поп-математика, Вопросы

---

Головоломки

[KingArthur]

Нашел в инете очень интересную головоломку.

www.sly2m.com/sly2m/rose/

Смыcл заключается в следующем: На основании значений 5 игральных костей нужно угадать сколько лепестков у розы...

У кого какие есть идеи? Просьба по гуглям не гулять... Там наверняка что то есть..

@темы: Головоломки и занимательные задачи

---

[Trotil]

47 мудрецов замышляли государственный переворот. Царь их построил в колонну, одев каждому на голову колпак: белый или черный. Спрашивает последнего (который видит 46 предыдущих): "Какого цвета на тебе колпак?" Отвечает правильно - остается в живых, нет - его убивают. Потом спрашивают второго (он видит уже 45 предыдущих) и так далее. Мудрецы имеют право договориться о тактике ответов, причем царь (расположенный к ним явно недружелюбно) их подслушивает, и все это знают. Понятно, что жизнь первого мудреца зависит от везения. Понятно, что если первый мудрец видит перед собой много черных колпаков и мало белых, то он скажет "черный" и тем спасет хотя бы половину своих друзей - они все будут говорить "черный". Можно ли еще как-то минимизировать человеческие потери?

@темы: Головоломки и занимательные задачи

---

Откуда минус?

[Trotil]

Мы хотим раскрыть скобки в следующем произведении:

(1 + x + x² + ... + x⁹) × (1 + x¹⁰ + x¹⁰ + ... + x⁹⁰) × (1 + x¹⁰⁰ + x²⁰⁰ + ... + x⁹⁰⁰) × ...

Заменяем каждую скобку на в точности равную ей дробь, получим:

(x¹⁰ - 1)/(x - 1) × (x¹⁰⁰ - 1)/(x¹⁰ - 1) × (x¹⁰⁰⁰ - 1)/(x¹⁰⁰ - 1) × ...

Сокращая равные множители в числителе и знаменателе, получаем, что начальное произведение равно

1/(x - 1) = - (1 + x + x² + x³ + ...)

Откуда минус?

@темы: Парадоксы, Головоломки и занимательные задачи

---

Аксиоматика арифметики

[Trotil]

falcao.livejournal.com/23149.html

@темы: Интересные ссылки

---

Что-то интересное..

[Trotil]

Что, точно не знаю

www.9151394.ru/projects/math/livegeom/pantuev/

На всякий случай опубликовываю, сейчас нет возможности изучить полностью страницу )))

@темы: Интересные ссылки

---

Задача

[Trotil]

В поезде Москва - Санкт-Петербург едут пассажиры Иванов, Петров и Сидоров. Такие же фамилии имеют машинист, проводник и кондуктор поездной бригады. Известно, что:
1. пассажир Иванов живет в Москве;
2. кондуктор живет на полупути от Москвы до Санкт-Петербурга;
3. пассажир, однофамилец кондуктора, живет в Санкт-Петербурге;
4. тот пассажир, который живет ближе к месту жительства кондуктора, чем другие пассажиры, зарабатывает в месяц ровно втрое больше кондуктора
5. пассажир Петров зарабатывает в месяц 200000 рублей;
6. Сидоров (из бригады) недавно выиграл у проводника партию на биллиарде.
Как фамилия машиниста?

@темы: Головоломки и занимательные задачи

---

Ну, раз уж совсем такая пьянка )))

[Amicus Plato]

Задачка бородатая. Может, кто-то и знает...

Задача про леммингов

На доске длиной 50 метров случайно расставили 128 леммингов. Доска достаточно узкая чтобы 2 лемминга не могли разойтись. Каждый лемминг движется со скоростью 50 метров в час (изначально одни идут вправо, другие влево, как расставили). Когда 2 лемминга встречаются они разворачиваются и расходятся в разные стороны. Когда лемминг доходит до края доски он падает и разбивается. Через какое время на доске гаранитрованно не останется ни одного лемминга?

@темы: Головоломки и занимательные задачи

---

Раз пошла такая пьянка...)

[Disprein]

Вот еще задачка.

На одномерную бесконечную ленту десантируют роботов. Лента поделена на ячейки. Требуется запрограммировать роботов так, чтобы они однажды собрались все вместе (в одной ячейке).

Каждый робот после посадки оставляет в месте приземления парашют.
Далее роботы начинают действовать в соответствии с заложенной в них программой. За один шаг программы робот может проверить, есть ли в его ячейке какой-нибудь парашют (но не может проверить, есть ли в ячейке другой робот!), и может при желании сдвинуться влево или вправо на одну ячейку. Программы всех роботов выполняются с одинаковой скоростью.
Количество роботов неизвестно. Но это количество — конечное число.

После того, как роботы соберутся вместе, не обязательно, чтобы они оставались в этом положении или остановились. Достаточно лишь, чтобы за конечное число шагов гарантированно наступила ситуация, когда все роботы находятся в одной и той же ячейке ленты.

@темы: Головоломки и занимательные задачи