Магический квадрат — это квадратная таблица n x n, заполненная n2 числами, таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях оказывается одинаковой.
Самый известный магический квадрат:
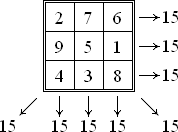
Оказывается, существует целая классификация магических квадратов. Итак:
Нормальный МК - магический квадрат, заполненный целыми числами от 1 до n2.
Полумагический квадрат - квадрат, заполненный числами от 1 до n2., называется полумагическим, если сумма чисел по горизонталям и вертикалям равна магической постоянной, а по диагоналям это условие не выполняется.
Aссоциативный, или симметричный МК, такой магический квадрат, у которого сумма любых двух чисел, симметрично расположенных относительно центра квадрата, равна одному и тому же числу: 1+n2.
Пандиагональный (дьявольский) МК - такой магический квадрат, в котором сумма чисел по разломанным диагоналям также равна константе квадрата.
Разломанные диагонали:

Идеальный МК - магический квадрат, который одновременно пандиагональный и ассоциативный.
Совершенный МК - магический пандиагональный квадрат порядка 4k, обладающий дополнительными свойствами.
Бимагический квадрат - такой магический квадрат, который остаётся магическим при замене всех его элементов на их квадраты. Бимагических квадратов 3,4,5 порядка не существует.
Мультимагический квадарат - обобщение бимагических квадратов на произвольную степень n.
По этой ссылке можно узнать количестве разных видов МК. Но там не учитываются изоморфные преобразования МК (когда один МК переходит в другой поворотом, сдвигом и т.д.) При подсчете они считались различными.
Самый известный магический квадрат:

Оказывается, существует целая классификация магических квадратов. Итак:
Нормальный МК - магический квадрат, заполненный целыми числами от 1 до n2.
Полумагический квадрат - квадрат, заполненный числами от 1 до n2., называется полумагическим, если сумма чисел по горизонталям и вертикалям равна магической постоянной, а по диагоналям это условие не выполняется.
Aссоциативный, или симметричный МК, такой магический квадрат, у которого сумма любых двух чисел, симметрично расположенных относительно центра квадрата, равна одному и тому же числу: 1+n2.
Пандиагональный (дьявольский) МК - такой магический квадрат, в котором сумма чисел по разломанным диагоналям также равна константе квадрата.
Разломанные диагонали:

Идеальный МК - магический квадрат, который одновременно пандиагональный и ассоциативный.
Совершенный МК - магический пандиагональный квадрат порядка 4k, обладающий дополнительными свойствами.
Бимагический квадрат - такой магический квадрат, который остаётся магическим при замене всех его элементов на их квадраты. Бимагических квадратов 3,4,5 порядка не существует.
Мультимагический квадарат - обобщение бимагических квадратов на произвольную степень n.
По этой ссылке можно узнать количестве разных видов МК. Но там не учитываются изоморфные преобразования МК (когда один МК переходит в другой поворотом, сдвигом и т.д.) При подсчете они считались различными.
-
-
30.05.2008 в 11:59так бы сразу и написал, что их там два!
-
-
30.05.2008 в 12:58Ведь числа не должны повторяться, как я понимаю. А там справа идентичный квадрат
Или они могут повторяться? Сам черт ногу сломит..
- По-моему, определение совершенного квадрата не должно зависеть от порядка квадрата.
- Тогда можно перефразировать - МК, обладающий такими-то свойствами - совершенен. Установлено, что такие квадраты могут быть только порядка 4k.
Нет, я не о том
Смотри, для 4 порядка набор свойств таков
Свойство 1. Сумма чисел в любом квадрате 2х2, находящемся внутри совершенного квадрата четвёртого порядка, равна магической константе квадрата.
Свойство 2. Сумма чисел, расположенных в угловых ячейках совершенного квадрата четвёртого порядка равна магической константе квадрата.
Свойство 3. Сумма чисел, расположенных в угловых ячейках любого квадрата 3х3, находящегося внутри совершенного квадрата четвёртого порядка, равна магической константе квадрата.
и т.д.
Для 8 порядка
Свойство 1. Сумма чисел в любом квадрате 2х2, находящемся внутри совершенного квадрата равна половине магической константы квадрата
Свойство2 . Сумма чисел в угловых ячейках совершенного квадрата восьмого порядка равна половине магической константы
Свойство 3. Сумма чисел в угловых ячейках любого квадрата 4х4, 5х5 и 6х6, находящихся внутри совершенного квадрата восьмого порядка, равна половине магической константы квадрата
Свойство 4. Если в совершенный квадрат восьмого порядка вписать квадрат 4х4 с вершинами в серединах сторон квадрата, то суммы чисел по каждой паре противоположных сторон вписанного квадрата будут равны магической константе квадрата
Видишь, набор свойств разный.
Я еще понимаю, если бы определение формулировалось как-то так: Магический квадрат порядка 4к называется совершенным, если
1) Сумма чисел в любом квадрате 2х2, находящемся внутри него, равна магической константе, деленной на к ( вряд ли это верно, но судя по этим двум примерам, по крайней мере для к=1,2 это выполняется. надо посмотреть, что там для к=3. Вроде для 12х12 на форуме писали, что построен совершенный квадрат)
ну и т.д.