Магический квадрат — это квадратная таблица n x n, заполненная n2 числами, таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях оказывается одинаковой.
Самый известный магический квадрат:
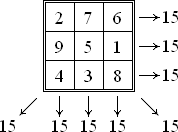
Оказывается, существует целая классификация магических квадратов. Итак:
Нормальный МК - магический квадрат, заполненный целыми числами от 1 до n2.
Полумагический квадрат - квадрат, заполненный числами от 1 до n2., называется полумагическим, если сумма чисел по горизонталям и вертикалям равна магической постоянной, а по диагоналям это условие не выполняется.
Aссоциативный, или симметричный МК, такой магический квадрат, у которого сумма любых двух чисел, симметрично расположенных относительно центра квадрата, равна одному и тому же числу: 1+n2.
Пандиагональный (дьявольский) МК - такой магический квадрат, в котором сумма чисел по разломанным диагоналям также равна константе квадрата.
Разломанные диагонали:

Идеальный МК - магический квадрат, который одновременно пандиагональный и ассоциативный.
Совершенный МК - магический пандиагональный квадрат порядка 4k, обладающий дополнительными свойствами.
Бимагический квадрат - такой магический квадрат, который остаётся магическим при замене всех его элементов на их квадраты. Бимагических квадратов 3,4,5 порядка не существует.
Мультимагический квадарат - обобщение бимагических квадратов на произвольную степень n.
По этой ссылке можно узнать количестве разных видов МК. Но там не учитываются изоморфные преобразования МК (когда один МК переходит в другой поворотом, сдвигом и т.д.) При подсчете они считались различными.
Самый известный магический квадрат:

Оказывается, существует целая классификация магических квадратов. Итак:
Нормальный МК - магический квадрат, заполненный целыми числами от 1 до n2.
Полумагический квадрат - квадрат, заполненный числами от 1 до n2., называется полумагическим, если сумма чисел по горизонталям и вертикалям равна магической постоянной, а по диагоналям это условие не выполняется.
Aссоциативный, или симметричный МК, такой магический квадрат, у которого сумма любых двух чисел, симметрично расположенных относительно центра квадрата, равна одному и тому же числу: 1+n2.
Пандиагональный (дьявольский) МК - такой магический квадрат, в котором сумма чисел по разломанным диагоналям также равна константе квадрата.
Разломанные диагонали:

Идеальный МК - магический квадрат, который одновременно пандиагональный и ассоциативный.
Совершенный МК - магический пандиагональный квадрат порядка 4k, обладающий дополнительными свойствами.
Бимагический квадрат - такой магический квадрат, который остаётся магическим при замене всех его элементов на их квадраты. Бимагических квадратов 3,4,5 порядка не существует.
Мультимагический квадарат - обобщение бимагических квадратов на произвольную степень n.
По этой ссылке можно узнать количестве разных видов МК. Но там не учитываются изоморфные преобразования МК (когда один МК переходит в другой поворотом, сдвигом и т.д.) При подсчете они считались различными.
-
-
29.05.2008 в 20:22Что-то мне не верится, что нормальных магических квадратов 4 порядка 880, пусть даже с учетом поворотов, сдвигов (а что такое сдвиг?)
По-моему, определение совершенного квадрата не должно зависеть от порядка квадрата. Иначе это каждый раз новое определение.
И все же по этой классификации ultramagic - это какой?
-
-
29.05.2008 в 20:33Пример: в пандиагональных квадратах если ты перенесешь последний столбец на место первого, он также останется магическим.
-
-
29.05.2008 в 22:30Спасибо огромное!
*Ничего, что я картинку прямо в текст воткнула?
-
-
29.05.2008 в 22:33Так тоже неплохо смотрится )
-
-
29.05.2008 в 22:49По рисунку это не особо понятно
(Извините, если вопрос тупой)
-
-
29.05.2008 в 22:56-
-
29.05.2008 в 23:00В трубочку вдоль или поперек?
А! То есть суммы крест накрест должны быть равны?
-
-
29.05.2008 в 23:00-
-
29.05.2008 в 23:02Я теперь скажу, как и аскеры)))
Ты говоришь загадками.
Amicus Plato
Вот ты его понимаешь с полуслова. А я нет(((
-
-
29.05.2008 в 23:04я просто убедительно умею делать вид, что понимаю )))
Ты никогда не играла в такую игрушку, которая называлась NetWalk? Там надо было комп. сеть собирать)))
Принцип был такой же)))
-
-
29.05.2008 в 23:08-
-
29.05.2008 в 23:10Нет, в такую игрушку не играла
Я в основном в стратегии играю
-
-
29.05.2008 в 23:12говорю же, я успешно делаю вид))) иногда не очень успешно)))
Объясняю.
Такая комп игрушка. Квадрат, разделенный на клетки. В одной клетке сервер, во всех остальных — либо компьютер (конец ветки), либо провод. Всё это хаотично разомкнуто. Ты собираешь из этого сеть. Так вот, на самом сложном уровне провода там можно замыкать через края. Как бы получается, что верх сомкнут с низом, а правое поле с левым.
Вот и всплыла аналогия)
Хорошая была игрушка... Эхх...
-
-
29.05.2008 в 23:16Ну да, прямо скажем, там вообще квадрата нет)))
Но если этот прямоугольник пристроить к себе же снизу или сверху, и поменять "диагонали" на границе направление на 90 градусов, то это самое оно и выйдет.
(если опять же, я правильно поняла)
-
-
29.05.2008 в 23:20или доходящие до центра, а потом поворачивающие?
в смысле до границы доходящие..
-
-
29.05.2008 в 23:22-
-
29.05.2008 в 23:27Мы с Amicus Plato за то, что отобразится симметрично
-
-
29.05.2008 в 23:27я уже сама не пойму, мы об одном и том же говорим? )))))
И о том же, о чем Тротил? )))
Я имела в виду вот что:
То есть если мы идем сначала из квадрата с единичкой и доходим до квадрата с семеркой, то оттуда мы попадаем в квадрат "15", и идем дальше вниз.
-
-
29.05.2008 в 23:2924 11 3 30 7 - одна из диагоналей. Так понятно?
Так понятно)))
А дальше как?
-
-
29.05.2008 в 23:29Нет, я точно не о том(((
-
-
29.05.2008 в 23:31-
-
29.05.2008 в 23:33А дальше никак. Все. Приехали. Диагональ кончилась.
-
-
29.05.2008 в 23:33а ты о чем?
Я так и подумала, что ты не о том....
И как люди такие квадраты по 45 лет изучают - ужас!
честно говоря, я б не смогла
-
-
29.05.2008 в 23:34Не понял...
Тогда зачем нам края загинать???
-
-
29.05.2008 в 23:36Тогда можно перефразировать - МК, обладающий такими-то свойствами - совершенен. Установлено, что такие квадраты могут быть только порядка 4k.
И все же по этой классификации ultramagic - это какой?
Идеальный, я так понимаю.
-
-
29.05.2008 в 23:38Чтобы перескочить из 3 в 20.
На картинке это решается преставлением такого же квадрата. А можно не преставлять, а свернуть в трубочку и продолжить.
-
-
29.05.2008 в 23:45Тьфу ты
Так здесь два рядом стоящих квадрата
А я думала, что один неполный размера 10х10..
-
-
29.05.2008 в 23:48Вот програмка: www.softpedia.com/get/Others/Home-Education/Mag...
Она находит все 880 квадратов
-
-
30.05.2008 в 11:49А я думала только половина ((((
Sensile
А я думала, что один неполный размера 10х10..
во-во! ))))
-
-
30.05.2008 в 11:58